 por creberson » Seg Jul 30, 2012 11:20
por creberson » Seg Jul 30, 2012 11:20
ola bom dia
prescizo de uma ajuda .
Determine a altura de uma piramide regular , de base pentagonal , sabendo que as suas arestas medem 10cm.
V= a\b = 1/3 100 cm v= a\b 100
-
creberson
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Jul 23, 2012 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
 por Russman » Seg Jul 30, 2012 14:02
por Russman » Seg Jul 30, 2012 14:02
Só aplicar o Teorema de Pitágoras.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por creberson » Ter Jul 31, 2012 22:14
por creberson » Ter Jul 31, 2012 22:14
não consegui entender o que voce postou,como usar o teorema de pitagoras? sendo que so tenho o valor da aresta , e não tenho valor da base.
-
creberson
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Jul 23, 2012 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
 por Russman » Ter Jul 31, 2012 22:28
por Russman » Ter Jul 31, 2012 22:28
Ao que parece todas as arestas do pirâmide medem 10 cm , incluindo as arestas da base.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por LuizAquino » Qui Ago 02, 2012 14:44
por LuizAquino » Qui Ago 02, 2012 14:44
creberson escreveu:Determine a altura de uma piramide regular , de base pentagonal , sabendo que as suas arestas medem 10cm.
V= a\b = 1/3 100 cm v= a\b 100
Russman escreveu:Só aplicar o Teorema de Pitágoras.
creberson escreveu:não consegui entender o que voce postou,como usar o teorema de pitagoras? sendo que so tenho o valor da aresta , e não tenho valor da base.
Russman escreveu:Ao que parece todas as arestas do pirâmide medem 10 cm , incluindo as arestas da base.
A figura abaixo ilustra o exercício.
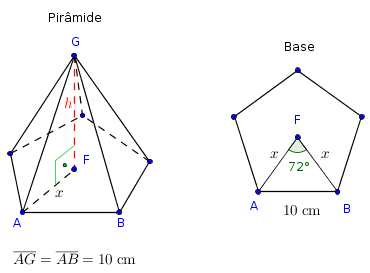
- figura.png (11.16 KiB) Exibido 2314 vezes
Note que você pode aplicar o Teorema de Pitágoras no triângulo retângulo AFG. A hipotenusa

mede 10 cm. O cateto

é o que você deseja calcular. Mas para calculá-lo você precisa descobrir o valor do cateto
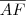
. Para descobri-lo, você aplicará a Lei dos Cossenos no triângulo isósceles AFB.
Tente usar essas informações para concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11733 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2838 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6137 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3148 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4192 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 mede 10 cm. O cateto
mede 10 cm. O cateto  é o que você deseja calcular. Mas para calculá-lo você precisa descobrir o valor do cateto
é o que você deseja calcular. Mas para calculá-lo você precisa descobrir o valor do cateto 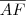 . Para descobri-lo, você aplicará a Lei dos Cossenos no triângulo isósceles AFB.
. Para descobri-lo, você aplicará a Lei dos Cossenos no triângulo isósceles AFB.