 por scoth » Sex Jul 20, 2012 20:07
por scoth » Sex Jul 20, 2012 20:07
Olá pessoal! questão longa mas que não consigo fechar.
Na ilustração ao lado, temos uma garrafa de café na forma cilíndrica com altura de 20 cm e largura de 12 cm e um coador na forma cônica com 13 cm da largura por 14 cm de altura. Além do corpo cilíndrico, a garrafa tem sua parte superior no formato de tronco de cone com 6 cm de altura e perímetro da boca igual a 6? cm. Suponha que, para preparar um café, o professor Eron colocou uma mistura de pó e açúcar no coador, observando que tal mistura ocupou 1/8 do espaço do coador. Em seguida, ele acrescentou rapidamente a água quente até a borda do coador. A partir dessas informações e admitindo o valor 3 como aproximação de ?, determine:
a) A quantidade de água, em litros, que o professor Eron despejou no coador.
b) O volume, em cm³, de pó de café e açúcar colocado no coador.
c) A diferença entre o volume de água despejado no coador e o volume de uma esfera de raio igual a 5,5 cm.
d) Para lavar a garrafa de café e o coador, o professor Eron gastou um volume de água equivalente ao volume das duas peças. Assim, considerando ? = 3, determine se a quantidade de água usada pode ser colocada, sem perdas, em um recipiente semi-esférico de raio igual a 10,5 cm
-
scoth
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jul 20, 2012 19:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Sex Jul 20, 2012 22:31
por Russman » Sex Jul 20, 2012 22:31
Você tentou fazer algo?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por scoth » Sex Jul 20, 2012 23:06
por scoth » Sex Jul 20, 2012 23:06
tentei e estou tentando, mas não consigo fechar, fico em duvida com o perímetro da boca e o volume das partes
-
scoth
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jul 20, 2012 19:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Dom Jul 22, 2012 21:18
por fraol » Dom Jul 22, 2012 21:18
Boa noite,
Vou palpitar na parte relacionada ao tronco de cone da parte superior da garrafa.
Nesse caso, temos na base do tronco um círculo de raio
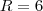
cm, pois a largura da garrafa é igual a 12 cm.
E temos no topo do tronco um círculo de raio

cm, pois o perímetro da boca é
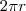
=

cm .
A fórmula para o volume desse tronco de cone é dado por
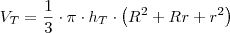
.
Daí em diante, sabido a fórmula para o cálculo do volume do cilindro (garrafa) =
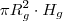
e para o cálculo do volume do cone (coador) =

é aplicar tais fórmulas para os dados fornecidos e fazer os cálculos.
Nas expressões acima temos

= tronco,

= garrafa,

= coador.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cilindro
por aprendiz » Dom Nov 09, 2008 23:10
- 0 Respostas
- 1299 Exibições
- Última mensagem por aprendiz

Dom Nov 09, 2008 23:10
Geometria Analítica
-
- Cilindro
por geriane » Qui Abr 22, 2010 16:21
- 1 Respostas
- 3422 Exibições
- Última mensagem por MarceloFantini

Qui Abr 22, 2010 17:35
Geometria Espacial
-
- Cilindro.
por nandokmx » Qua Jun 02, 2010 11:40
- 3 Respostas
- 2288 Exibições
- Última mensagem por MarceloFantini

Qui Jun 03, 2010 03:43
Geometria Espacial
-
- Cilindro
por renataf » Qua Dez 01, 2010 20:27
- 2 Respostas
- 6242 Exibições
- Última mensagem por renataf

Qui Dez 02, 2010 17:46
Geometria Espacial
-
- cilindro
por creberson » Qui Ago 16, 2012 21:34
- 1 Respostas
- 2734 Exibições
- Última mensagem por Russman

Qui Ago 16, 2012 22:16
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



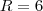 cm, pois a largura da garrafa é igual a 12 cm.
cm, pois a largura da garrafa é igual a 12 cm. cm, pois o perímetro da boca é
cm, pois o perímetro da boca é 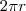 =
=  cm .
cm .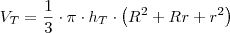 .
.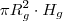 e para o cálculo do volume do cone (coador) =
e para o cálculo do volume do cone (coador) =  é aplicar tais fórmulas para os dados fornecidos e fazer os cálculos.
é aplicar tais fórmulas para os dados fornecidos e fazer os cálculos. = tronco,
= tronco,  = garrafa,
= garrafa,  = coador.
= coador.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.