 por Elson » Qui Fev 14, 2013 23:43
por Elson » Qui Fev 14, 2013 23:43
RESOLVA ESSA QUESTÃO DO CONCURSO CFOPM/BA
QUESTÃO43) Em um dia de grande movimentação em uma delegacia de polícia, o tempo médio e o tempo mediano de espera para atendimento de um grupo de 10 pessoas foram, ambos, iguais a 12 minutos.
Sabendo-se que o conjunto ordenado de valores 4,5,5,9,a,14,16,18,b,21 corresponde ao tempo de espera, em minutos, de cada uma dessas pessoas, pode-se concluir que b - a é igual a
01) 9
02) 8
03) 7
04) 6
05)5
RESPOSTA DO GABARITO 02)8
-
Elson
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Fev 12, 2013 23:19
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: gestão de recursos humanos
- Andamento: cursando
 por e8group » Sex Fev 15, 2013 21:04
por e8group » Sex Fev 15, 2013 21:04
Boa noite .Sabes oque é Mediana ? Se não por favor leia sobre isto
aqui :
Temos o conjunto ordenado contendo 10 elementos :
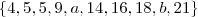
Como 10 é par o cálculo da mediana é dado entre os elementos

e

Ou seja, o cálculo da mediana será entre o quinto e sexto elemento do conjunto dado acima .
Quinto elemento : a
Sexto elemento : 14
Como sabemos que a mediana corresponde a 12 então

Por outro lado também sabemos que a média é 12 (mim) de um grupo de dez pessoas ;isto é ,
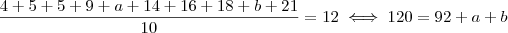
.
Queremos

certo ? Então,somando-se
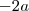
em ambos membros da igualdade ,
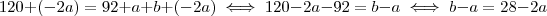
Ora ,mas como
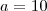
concluímos que
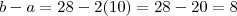
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Elson » Sáb Fev 16, 2013 00:06
por Elson » Sáb Fev 16, 2013 00:06
VALEU SANTHIAGO PELA AJUDA, UM ABRAÇOOOOOO!!!
-
Elson
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Fev 12, 2013 23:19
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: gestão de recursos humanos
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- RESOLVAAAA ESSA QUESTÃO CFOPM/BA
por Elson » Dom Fev 17, 2013 22:28
- 0 Respostas
- 950 Exibições
- Última mensagem por Elson

Dom Fev 17, 2013 22:28
Funções
-
- RESOLVAAAAA ESSA QUESTÃO CFOPM/BA
por Elson » Dom Fev 17, 2013 22:41
- 2 Respostas
- 2934 Exibições
- Última mensagem por Elson

Qua Fev 20, 2013 12:51
Análise Combinatória
-
- RESOLVER CFOPM/BA
por Elson » Qua Fev 13, 2013 00:00
- 3 Respostas
- 2281 Exibições
- Última mensagem por Cleyson007

Qui Fev 14, 2013 19:07
Funções
-
- resolva essa questão!
por leandro moraes » Qua Jul 07, 2010 09:45
- 12 Respostas
- 6138 Exibições
- Última mensagem por raitorres

Sex Mai 11, 2012 00:10
Funções
-
- (FGV) dúvida com essa questão
por Alex Rom » Qua Nov 17, 2010 18:47
- 3 Respostas
- 3061 Exibições
- Última mensagem por Alex Rom

Sáb Nov 27, 2010 13:39
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


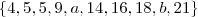
 e
e 

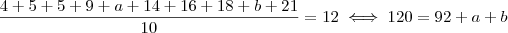 .
. certo ? Então,somando-se
certo ? Então,somando-se 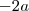 em ambos membros da igualdade ,
em ambos membros da igualdade ,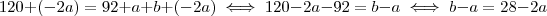
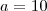 concluímos que
concluímos que 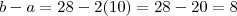

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
