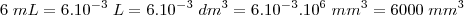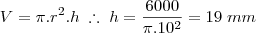por Carolziiinhaaah » Qui Set 02, 2010 14:50
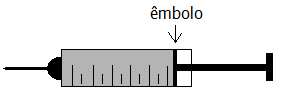
A figura abaixo representa uma seringa no formato de um cilindro circular reto, cujo êmbolo tem 20mm de diâmetro.
Esta seringa está completamente cheia de um medicamento e é usada para injetar doses de 6 ml desse medicamento.
Com basse nessas informações, determine quantos milímetros o êmbolo se desloca no interior da seinga ao ser injetada uma dose.
-
Carolziiinhaaah
- Usuário Parceiro
-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por Douglasm » Qui Set 02, 2010 18:19
Bom, você tem um volume de:
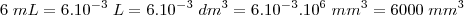
Você tem um cilindro de raio 10 mm e altura desconhecida:
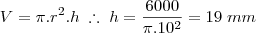
E é isso ai!
-
Douglasm
- Colaborador Voluntário
-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
