 por sergioh » Sex Abr 12, 2013 19:33
por sergioh » Sex Abr 12, 2013 19:33
Quem pode me ajudar nessa:
Concidere o retângulo ABCD. Uma rotação em torno de AB cria-se um cilindro de 96? cm³ e uma rotação em torno de AD um cilindro de 144? cm³. Calculo os lados do retângulo.
Resposta é: 4cm e 6 cm, mas não consigo chegar até elas.
obrigado!
-
sergioh
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Abr 01, 2013 18:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sex Abr 12, 2013 22:17
por young_jedi » Sex Abr 12, 2013 22:17
vamos dizer que um lado é x e o outro y
então
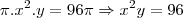
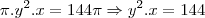
é so resolver o sistema, comente qualquer duvida
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por sergioh » Sáb Abr 13, 2013 17:11
por sergioh » Sáb Abr 13, 2013 17:11
Mas cara, ainda não consigo chegar aos resultados: 4cm e 6cm que tá no livro. Já tentei resolver o sistema mas... nada...!
Você conseguiu chegar nos resultados?
abraço!
-
sergioh
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Abr 01, 2013 18:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sáb Abr 13, 2013 21:08
por young_jedi » Sáb Abr 13, 2013 21:08
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- VOLUME DE UM CILINDRO
por sergioh » Sex Abr 12, 2013 19:38
- 0 Respostas
- 1420 Exibições
- Última mensagem por sergioh

Sex Abr 12, 2013 19:38
Geometria Espacial
-
- Volume do cilindro e da esfera
por Pri Ferreira » Sex Mai 18, 2012 23:24
- 0 Respostas
- 2306 Exibições
- Última mensagem por Pri Ferreira

Sex Mai 18, 2012 23:24
Geometria Espacial
-
- Geometria Espacial - Volume cilindro
por Reavourz » Qui Dez 11, 2014 10:24
- 1 Respostas
- 3743 Exibições
- Última mensagem por Molina

Qua Dez 17, 2014 14:13
Geometria Espacial
-
- [Volume de um cilindro circular reto]
por liahxs » Dom Ago 13, 2017 23:34
- 0 Respostas
- 4936 Exibições
- Última mensagem por liahxs

Dom Ago 13, 2017 23:34
Geometria Espacial
-
- [Volume] Volume de caixa para carrinho de mão
 por MateusDantas1 » Seg Nov 05, 2012 20:12
por MateusDantas1 » Seg Nov 05, 2012 20:12
- 0 Respostas
- 2732 Exibições
- Última mensagem por MateusDantas1

Seg Nov 05, 2012 20:12
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



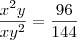
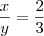
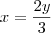
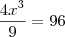
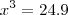
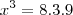
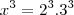

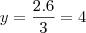


 , avisa que eu resolvo.
, avisa que eu resolvo.

