 por nathy vieira » Qua Out 07, 2009 23:18
por nathy vieira » Qua Out 07, 2009 23:18
Outra duvida : A caixa d'água tem a forma de um paralelepípedo retângulo e volume V. Mantidos o volume V e a profundidade 2m, se a largura BC for mudada para 2m, o comprimento AB deverá ser :
a- 7,0m
b- 5,5m
c- 6,0m
d- 6,5m
e- 7,5m
Obs : ab= 5m / bc= 3m e a profundidade 2m
Conto com a ajuda de vocês !
-
nathy vieira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Out 07, 2009 22:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Out 07, 2009 23:26
por Molina » Qua Out 07, 2009 23:26
Olá (novamente).
Você consegue definir o volume de um paralelepípedo com as dimensões 5m x 3m x 2m?
Esse volume ele que que mantenha, mas você vai modificar as dimensões do paralelepípedo:
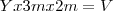
onde Y é essa medida que você terá que descobrir e V é o volume da caixa d'agua com as dimensões 5m x 3m x 2m.
Conseguiu?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por nathy vieira » Qua Out 07, 2009 23:38
por nathy vieira » Qua Out 07, 2009 23:38
Ainda não .
O volume do paralelepipedo vai ser 30 m?
se Y x 3m x 2m = 30 . Não consegui achar a resolução em nenhuma dessas alternativas acima !
-
nathy vieira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Out 07, 2009 22:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Out 08, 2009 14:17
por Molina » Qui Out 08, 2009 14:17
nathy vieira escreveu:Ainda não .
O volume do paralelepipedo vai ser 30 m?
se Y x 3m x 2m = 30 . Não consegui achar a resolução em nenhuma dessas alternativas acima !
Sim, o volume da caixa d'água é
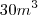
.
Eu digitei errado, na verdade é Y x 2m x 2m = 30.
O primeiro 2m é referente a profundidade e o outro 2m é referente ao lado BC (que foi diminuido).
Agora dá certo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por nathy vieira » Qui Out 08, 2009 18:37
por nathy vieira » Qui Out 08, 2009 18:37
Ah sim , agora consegui entender .
Obrigada mais uma vez !
-
nathy vieira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Out 07, 2009 22:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11735 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2844 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3156 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4201 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
-
- Geometria espacial
por nayara michele » Ter Set 27, 2011 17:43
- 1 Respostas
- 2392 Exibições
- Última mensagem por Neperiano

Ter Set 27, 2011 18:02
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


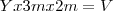


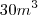 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
