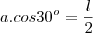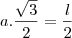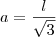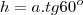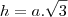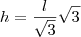Geometria - Volume de um prisma

por **Janffs** » Qui Nov 15, 2012 18:14

Procurando uma embalagem diferenciada para o lançamento de um perfume, um design usa uma prisma triangular com as seguintes caracteristicas:

- a base do prisma é um triangulo equilatero de lado l u.c;
- um dos vertices da base superior projeta-se no centro da base inferior;
- as arestas laterais formam 60º com o plano da base;

Nessas condições, o volume do prisma em u.v., é igual a

- eu sei que o volume de um prisma é dado por:

V= area da base x altura

- sei que a area de um triangulo equilatero é

$\frac{{l}^{2} \sqrt[]{3}}{4}$

- mas não tó conseguindo achar a altura do prisma

Alguem ajuda por favor! :-P

por **young_jedi** » Qui Nov 15, 2012 20:36

: prisma.png (4.81 KiB) Exibido 3163 vezes

utilizando a figura nos vemos que

$a.cos30^o=\frac{l}{2}$

$a.\frac{\sqrt3}{2}=\frac{l}{2}$

$a=\frac{l}{\sqrt3}$

e olhando a figura do prisma nos vemos que a altura h

h=a.tg60^o

$h=a.\sqrt3$

$h=\frac{l}{\sqrt3}\sqrt3$

h=l

Geometria - Volume de um prisma

Geometria - Volume de um prisma

Geometria - Volume de um prisma

Re: Geometria - Volume de um prisma

Quem está online