 por samra » Qui Set 20, 2012 13:33
por samra » Qui Set 20, 2012 13:33
Olá pessoal,
como eu faço pra esboçar o ponto (0,0,0) no plano tridimensional?
(Eu achava q era a origem do plano, mas meu prof disse que não é)

Se tiver como, coloquem uma imagem, por favor, pra ficar mais fácil a visualização,
Obrigada. att.
Samara
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por MarceloFantini » Qui Set 20, 2012 13:38
por MarceloFantini » Qui Set 20, 2012 13:38
Isto é a origem do sistema cartesiano tridimensional, que não é um plano. Qual é o enunciado completo?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por samra » Qui Set 20, 2012 20:28
por samra » Qui Set 20, 2012 20:28
O enunciado é:
Represente x=0 , y = 0 e Z=0 no R³ .
Aí eu perguntei pro prof se o ponto é (0,0,0), ele disse q sim, que deveríamos representar esse ponto.
No desenho q ele esboçou para representar esse ponto, ficou parecendo um cubo, porém tracejado... Ele ainda completou dizendo q
no plano (x,y), qdo um dos termos é zero, e o outro varia, o esboço seria o eixo que está variando. (aí fiquei na dúvida porque no caso
de ser (0,0), significa que o ponto está na origem). Mas ele disse que no caso do plano tridimensional, este ponto seria os três eixos juntos, por isso o desenho parece um cubo.
Mas estou na dúvida... help me?
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por MarceloFantini » Qui Set 20, 2012 21:20
por MarceloFantini » Qui Set 20, 2012 21:20
As equações
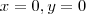
e

representam planos em

, que são o plano
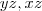
e

respectivamente. A interseção desses três planos é a origem. Tente fazer o desenho pensando nisso agora.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por samra » Sáb Out 06, 2012 15:43
por samra » Sáb Out 06, 2012 15:43
sim. Obrigada
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14950 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
-
- Distancia entre ponto e plano
por teneral » Seg Jul 09, 2018 11:29
- 0 Respostas
- 5361 Exibições
- Última mensagem por teneral

Seg Jul 09, 2018 11:29
Geometria Analítica
-
- [Geometria Analítica] Projeção do ponto no plano
 por -civil- » Qui Ago 11, 2011 09:51
por -civil- » Qui Ago 11, 2011 09:51
- 1 Respostas
- 2982 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 13:14
Geometria Analítica
-
- Dúvida... A prova é hoje (Distância entreo ponto e o plano)
por valeuleo » Ter Mai 10, 2011 12:20
- 1 Respostas
- 1588 Exibições
- Última mensagem por LuizAquino

Qua Mai 11, 2011 10:30
Geometria Analítica
-
- [CURVAS] Gráfico da função, ponto mais próximo de um plano
 por inkz » Qui Nov 22, 2012 02:49
por inkz » Qui Nov 22, 2012 02:49
- 4 Respostas
- 4678 Exibições
- Última mensagem por inkz

Sáb Nov 24, 2012 08:51
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







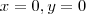 e
e  representam planos em
representam planos em  , que são o plano
, que são o plano 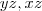 e
e  respectivamente. A interseção desses três planos é a origem. Tente fazer o desenho pensando nisso agora.
respectivamente. A interseção desses três planos é a origem. Tente fazer o desenho pensando nisso agora.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
