Pessoal, eu tenho a resolução desse exercício. Estou aqui justamente para que alguém me ajude a entender um determinado trecho da resolução. Vou postar toda a resolução e vou mostrar depois o que eu não entendi.
'' O poliedro possui p faces triangulares e q faces quadrangulares. Disso vem:
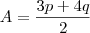
Agora a parte que eu não entendi:
''Em 6 vértices concorrem (q+1) arestas e nos outros dois
arestas. Cada aresta esta contida em 2 vértices distintos, ou seja, essa expressão corresponde ao dobro da quantidade de arestas do poliedro . 6 (q+1) + 2(p/2) = 2A sendo A o número de arestas.
O que eu não entendi é justamente porque a expressão corresponde ao dobro do número de arestas e onde que ''e nos outros dois
arestas'' entra nessa história... Muito grato se puderem ajudar, pois não passei frente porque empaquei nisso.
por 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.