[Segmentos de reta paralelos] - Como achar coordenadas

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Segmentos de reta paralelos] - Como achar coordenadas

Regras do fórum
Responder

[Segmentos de reta paralelos] - Como achar coordenadas

Mensagempor liviozanol » Qua Mai 09, 2012 00:30

Boa noite!

Tem muito tempo que não exercito minha trigonometria (acho que desde o segundo grau) e preciso de um auxílio. Será que alguma alma caridosa pode me ajudar?

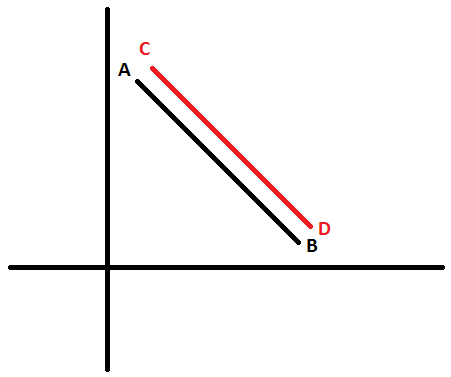
Tenho um segmento de reta AB em um plano determinado através dos pontos (x1,y1) e (x2,y2). Preciso saber as coordenadas (x1',y1') e (x2',y2') de um outro segmento de reta CD de mesmo tamanho paralelo a AB e distanciado em 5 deste. Gostaria de saber qual fórmula devo utilizar para saber os pontos " X' e Y' " do segmento CD.

Sei que para saber o tamanho de AB basta usar o teorema de pitágoras, mas como achar as coordenadas de CD?

Figura em anexo.

Ficarei muito grato se alguém puder ajudar.
Anexos
segmentos paralelos.png
segmentos paralelos
segmentos paralelos.png (5.53 KiB) Exibido 1094 vezes
liviozanol
Novo Usuário
Novo Usuário
 
Mensagens: 1
Registrado em: Qua Mai 09, 2012 00:16
Formação Escolar: GRADUAÇÃO
Área/Curso: c. da computacao
Andamento: formado
Voltar ao topo
Responder

Voltar para Geometria Espacial

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum