Estou estudando para a segunda etapa do vestibular da ufmg, e travei numa questão de matemática da prova de 2001.
Segue a questão (creio que a figura é desnecessária para minha dúvida):
Nessas figuras, estão representados os recipientes I e II.
O recipiente I está completamente cheio de água e tem a forma de um cone circular reto, com altura H e raio da base R1.
O recipiente II está vazio e também tem a forma de um cone circular reto, com a mesma altura H , mas com raio da base igual a R2.
A água contida em I é, então, vertida em II, até que o nível da água, em ambos os recipientes, tenha a mesma altura h.
Considerando essas informações, ESCREVA essa altura h em função de H, R1 e R2.
A apostila da Editora Bernoulli traz a seguinte resposta
![h= H\sqrt[3]{\frac{{R1}^{2}}{{R1}^{2}+{R2}^{2}}} h= H\sqrt[3]{\frac{{R1}^{2}}{{R1}^{2}+{R2}^{2}}}](/latexrender/pictures/824f22ebab54d0d88ade9b0988e63b9f.png)
Tentei realizar a questão por meio de semelhança entre os volumes de cada cone, assim como também igualar com a semelhança do outro cone pois os dois ao meu ver tem a mesma constante cúbica.
Como seria o melhor modo de resolver essa questão?


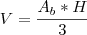 em que
em que  é a área da base e
é a área da base e  é a altura
é a altura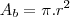


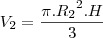
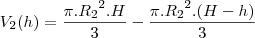



 .
.
 :
: