 por renataf » Seg Nov 29, 2010 10:06
por renataf » Seg Nov 29, 2010 10:06
uma caixa na forma de um paralelepípedo de base quadrada contém uma pirâmide, cujos vértices da base são os pontos médios das arestas do fundo da caixa. O vértice superior da pirâmide toca a tampa da caixa. A razão entre os volumes da pirâmide e da caixa é igual a:
A)1/3
B)1/4
C)1/6
D)1/8
E)1/12
A resposta correta é a C, mas eu tentei fazer e só consigo chegar na letra E.
Minha resolução fica assim;
O volume da pirâmide:
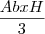
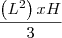
(já q a base da pirâmide está inserida numa caixa de base quadrada, logo a base da pirâmide é um quadrado)
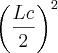
x
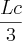
(eu coloquei lado da caixa sobre 2 pq ele diz q os vértices da base são os pontos médios das arestas do fundo da caixa e H=lado da caixa pq a piramide esta inserida na caixa e a ponta dela bate na tampa da caixa)
Resolvendo fica:
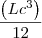
O volume da caixa é :
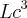
a razao:
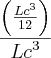
Aí vai ficar:

Não sei no que estou errando. Gostaria q alguém me ajudasse.
-
renataf
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Sáb Nov 20, 2010 17:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fttofolo » Seg Nov 29, 2010 10:36
por fttofolo » Seg Nov 29, 2010 10:36
Temos que o volume do paralelepípedo é:
V=a^2.h (área da base x altura), como a base é um quadrado de lado a.
A base da pirâmide tem seus vértices nos pontos médios do quadrado do paralelepípedo, logo
a base da pirâmide vai ser um quadrado inscrito no quadrado do paralelepípedo (ver figura em anexo)
Então usamos a fórmula da diagonal para descobrirmos o valor do lado da base da pirâmide:
![d=l\sqrt[2]{2} d=l\sqrt[2]{2}](/latexrender/pictures/36913f394e0e1917e6c2b3db67122e35.png)
![a=l\sqrt[2]{2} a=l\sqrt[2]{2}](/latexrender/pictures/7591af6f527596fd2499f72ba054e0fb.png)
![l=\frac{a\sqrt[2]{2}}{a} l=\frac{a\sqrt[2]{2}}{a}](/latexrender/pictures/21854a97f9c8d2cadfc20285485e0eb5.png)
Temos que oo volume do paralelepípedo é
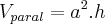
Temos que o volume da pirâmide é
![{V}_{piram}=\frac{1}{3}{\left(\frac{a\sqrt[2]{2}}{2} \right)}^{2} {V}_{piram}=\frac{1}{3}{\left(\frac{a\sqrt[2]{2}}{2} \right)}^{2}](/latexrender/pictures/096ca223c0fcfb2c064ee7db605ed269.png)

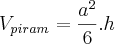
Razão entre volumes:
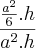
Logo a razão vai ser

- Anexos
-
[O anexo não pode ser exibido, pois a extensão pdf foi desativada pelo administrador.]
-
fttofolo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Sex Nov 19, 2010 10:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por renataf » Seg Nov 29, 2010 10:52
por renataf » Seg Nov 29, 2010 10:52
Obrigada pela ajuda! Foi falta de atenção minha.
-
renataf
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Sáb Nov 20, 2010 17:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fttofolo » Seg Nov 29, 2010 11:09
por fttofolo » Seg Nov 29, 2010 11:09
Percebo que a maioria das pessoas (inclusive eu), não prestamos atenção a detalhes e as vezes cometemos erros, tenho procurado me policiar mais, pois leio com muita pressa e muitas vezes acabo errando.
-
fttofolo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Sex Nov 19, 2010 10:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Espacial - Pirâmide] Pirâmide de Cartolina
por raimundoocjr » Qui Ago 02, 2012 22:13
- 1 Respostas
- 2699 Exibições
- Última mensagem por MarceloFantini

Qui Ago 02, 2012 23:04
Geometria Espacial
-
- piramide
 por Gir » Ter Set 22, 2009 12:01
por Gir » Ter Set 22, 2009 12:01
- 2 Respostas
- 2849 Exibições
- Última mensagem por Gir

Qua Set 23, 2009 11:02
Geometria Espacial
-
- Pirâmide
por Ani » Dom Dez 05, 2010 15:12
- 4 Respostas
- 3540 Exibições
- Última mensagem por Elcioschin

Sex Dez 10, 2010 21:42
Geometria Espacial
-
- Pirâmide
por Cleison » Seg Mai 16, 2011 17:11
- 1 Respostas
- 1567 Exibições
- Última mensagem por LuizAquino

Ter Jun 21, 2011 23:21
Geometria Espacial
-
- piramide!
por willwgo » Sex Jul 08, 2011 18:19
- 0 Respostas
- 2859 Exibições
- Última mensagem por willwgo

Sex Jul 08, 2011 18:19
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
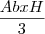
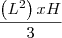 (já q a base da pirâmide está inserida numa caixa de base quadrada, logo a base da pirâmide é um quadrado)
(já q a base da pirâmide está inserida numa caixa de base quadrada, logo a base da pirâmide é um quadrado)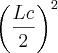 x
x 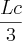 (eu coloquei lado da caixa sobre 2 pq ele diz q os vértices da base são os pontos médios das arestas do fundo da caixa e H=lado da caixa pq a piramide esta inserida na caixa e a ponta dela bate na tampa da caixa)
(eu coloquei lado da caixa sobre 2 pq ele diz q os vértices da base são os pontos médios das arestas do fundo da caixa e H=lado da caixa pq a piramide esta inserida na caixa e a ponta dela bate na tampa da caixa)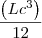
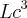
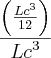



![d=l\sqrt[2]{2} d=l\sqrt[2]{2}](/latexrender/pictures/36913f394e0e1917e6c2b3db67122e35.png)
![a=l\sqrt[2]{2} a=l\sqrt[2]{2}](/latexrender/pictures/7591af6f527596fd2499f72ba054e0fb.png)
![l=\frac{a\sqrt[2]{2}}{a} l=\frac{a\sqrt[2]{2}}{a}](/latexrender/pictures/21854a97f9c8d2cadfc20285485e0eb5.png)
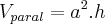
![{V}_{piram}=\frac{1}{3}{\left(\frac{a\sqrt[2]{2}}{2} \right)}^{2} {V}_{piram}=\frac{1}{3}{\left(\frac{a\sqrt[2]{2}}{2} \right)}^{2}](/latexrender/pictures/096ca223c0fcfb2c064ee7db605ed269.png)

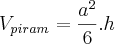
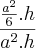


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.