 por JessicaHayanne » Qua Jun 20, 2012 13:20
por JessicaHayanne » Qua Jun 20, 2012 13:20
Boa tarde..
Alguem poderia me auxiliar.. *-*
tenho um trabalho envolvendo as duas disciplinas, tenho que fazer a 'plotagem' de uma elipse no winplot onde ocorra uma expansão (ou contração) da mesma, porém para isso necessito encontrar a matriz de transformação linear de expansão ( ou contração)..
Já obti a paramétrica dela que é:
E : � x = xo+acos(t)
y = yo+bsin(t)
Sei que preciso dela .. porém nao sei como aplica-la na transformação! "/
Alguem que ja tenha feito ou saiba Por Favor me ajude preciso com extrema importância e urgência..
Grata desde ja'
-
JessicaHayanne
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jun 20, 2012 13:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Dom Jun 24, 2012 08:37
por LuizAquino » Dom Jun 24, 2012 08:37
JessicaHayanne escreveu:Boa tarde..
Alguem poderia me auxiliar.. *-*
tenho um trabalho envolvendo as duas disciplinas, tenho que fazer a 'plotagem' de uma elipse no winplot onde ocorra uma expansão (ou contração) da mesma, porém para isso necessito encontrar a matriz de transformação linear de expansão ( ou contração)..
Já obti a paramétrica dela que é:
E : x = xo+acos(t)
y = yo+bsin(t)
Sei que preciso dela .. porém nao sei como aplica-la na transformação! "/
Alguem que ja tenha feito ou saiba Por Favor me ajude preciso com extrema importância e urgência..
A matriz da transformação é dada por:
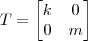
Se k > 1, então temos uma expansão na direção do eixo x. Mas se 0 < k < 1, então temos uma contração na direção do eixo x.
Se m > 1, então temos uma expansão na direção do eixo y. Mas se 0 < m < 1, então temos uma contração na direção do eixo y.
Se você usar k = m, então ocorrerá ao mesmo tempo uma expansão ou uma contração em ambas as direções.
Os pontos (x, y) da elipse resultante ao aplicar essa transformação serão dados por:
 Observação
ObservaçãoPara plotar os gráficos eu recomendo o
GeoGebra.
Se você desejar um tutorial sobre esse programa, então eu gostaria de recomendar os vídeos que estão disponíveis no meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Algebra linear e geometria analítica
por clari_27 » Sáb Mai 12, 2012 17:32
- 1 Respostas
- 1905 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 10:56
Geometria Analítica
-
- Geometria Analitica e Algebra linear
por Danizinhalacerda13 » Qui Mai 01, 2014 19:15
- 1 Respostas
- 2898 Exibições
- Última mensagem por Danizinhalacerda13

Qui Mai 01, 2014 19:25
Geometria Analítica
-
- Algebra linear e geometria analitica. Me ajudem!!!
por clari_27 » Sáb Mai 12, 2012 17:19
- 1 Respostas
- 1835 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 10:48
Geometria Analítica
-
- [Algebra linear e geometria analitica] Duvida
por lucasdemirand » Sáb Jul 06, 2013 15:32
- 1 Respostas
- 1402 Exibições
- Última mensagem por e8group

Dom Jul 07, 2013 21:27
Álgebra Linear
-
- Geometria Analitica e Algebra linear-O plano - Ajuda
por Danizinhalacerda13 » Qui Mai 01, 2014 20:37
- 3 Respostas
- 2421 Exibições
- Última mensagem por Cleyson007

Sáb Mai 03, 2014 10:15
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


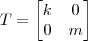




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.