Boa noite,
Izabela.
Primeiramente perceba que ambas são do primeiro grau por se tratar de retas.
Outra informação que nos ajuda é que r é reta, então pode ser escrita pela forma
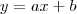
.
Sabemos também que
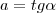
m onde

é o ângulo entre a reta r e o eixo x.
Precisamos então achar este ângulo da reta r primeiramente. Note na sua imagem, um triângulo formado pelas retas e o eixo x. O ângulo superior é oposto ao vértice do 105º, logo aquele ângulo vale
105º. O ângulo do lado direito do triângulo é suplementar ao 135º, logo vale
45º. O último ângulo (que nos interessa) é
30º, pois 105º + 45º + 30º = 180º (soma dos ângulos internos de um triângulo).
Ache
a agora e lembre-se que o valor do
b é onde a reta intercepta o eixo y.
Faça um procedimento parecido para a outra reta, porém, você terá que igualar as funções para encontrar o valor de
b.
Qualquer dúvida, avise!





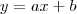 .
.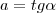 m onde
m onde  é o ângulo entre a reta r e o eixo x.
é o ângulo entre a reta r e o eixo x.



 , avisa que eu resolvo.
, avisa que eu resolvo.

