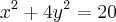 , para que os valores de m a reta
, para que os valores de m a reta 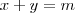
a)Corta a elipse
b)É tangente a elipse
c)Não corta a elipse
Não sei como fazer.
cheguei a transformar a equação da elipse em
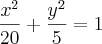

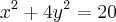 , para que os valores de m a reta
, para que os valores de m a reta 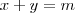
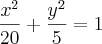

Claudin escreveu:Em relação a elipse, para que os valores de m a reta
a)Corta a elipse
b)É tangente a elipse
c)Não corta a elipse
Claudin escreveu:Não sei como fazer.
cheguei a transformar a equação da elipse em
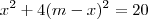
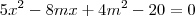
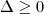 ), temos que a reta irá cortar a elipse.
), temos que a reta irá cortar a elipse. ), temos que a reta será tangente a elipse.
), temos que a reta será tangente a elipse.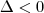 ), temos que a reta não cortará a elipse.
), temos que a reta não cortará a elipse.

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

