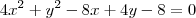
Reduzindo a equação encontrei:
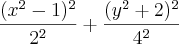
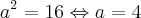 logo,
logo,  (Eixo Maior)
(Eixo Maior) logo,
logo,  (Eixo Menor)
(Eixo Menor)![a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3} a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3}](/latexrender/pictures/24871e492b7e1a72d83cf46caef3de5d.png) logo,
logo, ![F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3} F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3}](/latexrender/pictures/655d5c44d05a84ca22485d2be9e01bf6.png)
![e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2} e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2}](/latexrender/pictures/9ad7d03db6662451ecc8bb28ef368612.png)
Portanto:
![F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3}) F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3})](/latexrender/pictures/6f2d35ea939a773dfd996f7addd7cefc.png)
![F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3}) F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3})](/latexrender/pictures/31ccee643396e87cd8f4feaa7f4cc6d8.png)
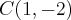 ou
ou  Não sei direito qual o certo.
Não sei direito qual o certo.E os valores de
 e
e  também não consegui encontrar.
também não consegui encontrar.
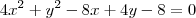
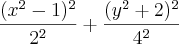
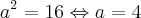 logo,
logo,  (Eixo Maior)
(Eixo Maior) logo,
logo,  (Eixo Menor)
(Eixo Menor)![a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3} a^2=b^2+c^2 \Leftrightarrow c=2\sqrt[]{3}](/latexrender/pictures/24871e492b7e1a72d83cf46caef3de5d.png) logo,
logo, ![F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3} F_1F_2 = 2c \Leftrightarrow 4\sqrt[]{3}](/latexrender/pictures/655d5c44d05a84ca22485d2be9e01bf6.png)
![e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2} e=\frac{c}{a}\Leftrightarrow e = \frac{\sqrt[]{3}}{2}](/latexrender/pictures/9ad7d03db6662451ecc8bb28ef368612.png)
![F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3}) F_1(x_o, y_o-c) = (1,-2-2\sqrt[]{3})](/latexrender/pictures/6f2d35ea939a773dfd996f7addd7cefc.png)
![F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3}) F_2(x_o, y_o+c) = (1,-2+2\sqrt[]{3})](/latexrender/pictures/31ccee643396e87cd8f4feaa7f4cc6d8.png)
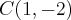 ou
ou  Não sei direito qual o certo.
Não sei direito qual o certo. e
e  também não consegui encontrar.
também não consegui encontrar.
 ou
ou 
 ou
ou 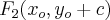


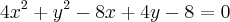 ================>
================> 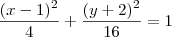
 ========>
========> 
 =====>
=====>  =====>
=====> 
![c = 2\sqrt[]{3} c = 2\sqrt[]{3}](/latexrender/pictures/e5fdf170109e325b5b5ec3b1b6448b34.png) e
e ![c = - 2\sqrt[]{3} c = - 2\sqrt[]{3}](/latexrender/pictures/6fd996dda7a1838987ee0a9527682098.png)
![(1, - 2\sqrt[]{3}) (1, - 2\sqrt[]{3})](/latexrender/pictures/3b1a2c2c81e72983e0f05ee4d0bcae6e.png) e
e ![(1, 2\sqrt[]{3}) (1, 2\sqrt[]{3})](/latexrender/pictures/38b7253682996bd9ca117ce153b1ad09.png)

![(1,-2+2\sqrt[]{3}) (1,-2+2\sqrt[]{3})](/latexrender/pictures/e36818cc89a8e23200a67376c93f297c.png)
![(1,-2-2\sqrt[]{3}) (1,-2-2\sqrt[]{3})](/latexrender/pictures/734aaba5806486a77f0164b1cd96fe41.png)

Claudin escreveu:Os focos não seriam:
E ainda não consegui entender como chegar nesses resultados dos vértices, não sei como encontrar.



Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.