Fabio Wanderley escreveu:2.65) Determine uma equação da circunferência tangente às retas y = x e y = -x nos pontos (3,3) e (-3,3).
Fabio Wanderley escreveu:Eu tentei encontrar o ponto do centro da circunferência, mas só consegui concluir que
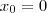
(calculando a distância da origem aos pontos pertencentes à reta).
Alguém pode me ajudar?
Para resolver esse exercício, siga os passos:
1) Determine a reta que passa pelo ponto (3, 3) e é perpendicular a reta y = x;
2) Determine a reta que passa pelo ponto (-3, 3) e é perpendicular a reta y = -x;
3) Determine o ponto de interseção entre as retas encontradas nos passos 1) e 2). Esse ponto corresponde ao centro da circunferência procurada;
4) Calcule a distância entre o ponto encontrado no passo 3) e o ponto (3, 3) (ou a distância ao ponto (-3,3) se preferir). Essa distância corresponde ao raio da circunferência procurada;
5) Considerando o centro encontrado no passo 3) e o raio no passo 4), determine a equação da circunferência procurada.
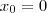 (calculando a distância da origem aos pontos pertencentes à reta).
(calculando a distância da origem aos pontos pertencentes à reta).



