


 uma função definida da seguinte forma para o intervalo
uma função definida da seguinte forma para o intervalo ![[0,c] [0,c]](/latexrender/pictures/0b77a0c57e4d83ea934d4ef032e10c08.png)
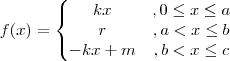
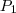 e
e  :
:
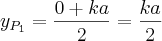
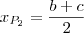
 .
.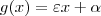 e mostrar que a mesma é nula, isto é, a reta que liga os pontos
e mostrar que a mesma é nula, isto é, a reta que liga os pontos 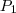 e
e  é paralela ao eixo x onde se estende a base maior do trapézio. Identificando o sistema, temos
é paralela ao eixo x onde se estende a base maior do trapézio. Identificando o sistema, temos
 podemos simplificar o sistema para
podemos simplificar o sistema para
 . Portanto, ou
. Portanto, ou  ( identicamente 0, isto é, 0 para todo intervalo) ou
( identicamente 0, isto é, 0 para todo intervalo) ou  . Como por hipótese
. Como por hipótese  e são todos positivos, a segunda alternativa é descartada. Assim, provamos que
e são todos positivos, a segunda alternativa é descartada. Assim, provamos que  para quaisquer valores de a,b e c e , portanto, que a reta que liga os pontos médios é paralela as bases do trapézio.
para quaisquer valores de a,b e c e , portanto, que a reta que liga os pontos médios é paralela as bases do trapézio.
 o comprimento da curva
o comprimento da curva . Então:
. Então: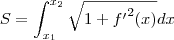 .
. é
é 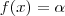 definida para o intevalo
definida para o intevalo ![[\frac{a}{2},\frac{b+c}{2}] [\frac{a}{2},\frac{b+c}{2}]](/latexrender/pictures/6591efc199829bfb94052a2591b88746.png) . Assim, o comprimento
. Assim, o comprimento  é portanto
é portanto , uma vez que
, uma vez que  é uma constante e sua derivada com relação a
é uma constante e sua derivada com relação a  é nula.
é nula. e o da base menor é
e o da base menor é  . Assim, a média aritimética entre eles é
. Assim, a média aritimética entre eles é  . Este valor é exatamente o comprimento da reta que liga os pontos médios. Portanto está demosntrado o enunciado.
. Este valor é exatamente o comprimento da reta que liga os pontos médios. Portanto está demosntrado o enunciado.
Guilherme Carvalho escreveu:Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo às bases, e sua medida é a média aritmética das medidas das bases.
Russman escreveu:Vamos construir um trapézio analiticamente, isto é, construir uma função que quando observado seu gráfico tenhamos a forma de um trapézio!
Sejauma função definida da seguinte forma para o intervalo
Os pontos médios dos lados adjacentes são calculados respectivamente pore
:
.
Agora temos de calcular a declividade da retae mostrar que a mesma é nula, isto é, a reta que liga os pontos
e
é paralela ao eixo x onde se estende a base maior do trapézio. Identificando o sistema, temos
Observando-se quepodemos simplificar o sistema para
de onde, após um processo algébrico, chega-se em. Portanto, ou
( identicamente 0, isto é, 0 para todo intervalo) ou
. Como por hipótese
e são todos positivos, a segunda alternativa é descartada. Assim, provamos que
para quaisquer valores de a,b e c e , portanto, que a reta que liga os pontos médios é paralela as bases do trapézio.
 ) está ok. Mas na definição da função f, no intervalo (b, c], não necessariamente o coeficiente angular é -k.
) está ok. Mas na definição da função f, no intervalo (b, c], não necessariamente o coeficiente angular é -k.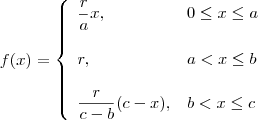
 . Mas e se eles estiverem em
. Mas e se eles estiverem em  ?
?Russman escreveu:Para calcular a medida da reta que liga os pontos médios usemos, por formalidade, a fórmula que calcula o comprimento de uma curva plana contínua para algum interválo e suficientemente diferenciável. Sejao comprimento da curva
. Então:
.
A funçãoé
definida para o intevalo
. Assim, o comprimento
é portanto
, uma vez que
é uma constante e sua derivada com relação a
é nula.
Veja, agora, que o comprimento da base maior ée o da base menor é
. Assim, a média aritimética entre eles é
. Este valor é exatamente o comprimento da reta que liga os pontos médios. Portanto está demosntrado o enunciado.


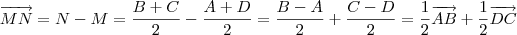
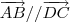 , existe um escalar k (diferente de zero, pois
, existe um escalar k (diferente de zero, pois  e
e  não são vetores nulos), tal que
não são vetores nulos), tal que  .
.
 , com
, com 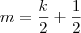 , temos que
, temos que 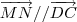 . Já que também temos que
. Já que também temos que  , teremos então que
, teremos então que 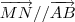 .
.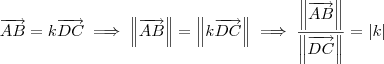



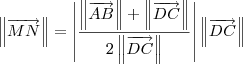


 ou
ou  .
.
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.