jmontenegro escreveu:Os pontos A(2,1) e B(0,3) pertencem à elipse E. A elipse E’foi obtida por uma homotetia de centro na origem do sistema de coordenadas.
(a imagem referente ao problema está em
http://imageshack.us/photo/my-images/802/problemaq.jpg)
Os pontos A’ e B’ são, respectivamente, as imagens de A e B por essa homotetia. O ponto B’ pertence ao eixo das ordenadas e tem abscissa igual a 1.
O ponto A’ pertence à reta s, perpendicular a reta AA’. A equação geral da reta s é:
(A) 12x + 6y ? 5 = 0
(B) 12x + 6y + 3 = 0
(C) 6x + 3y + 5 = 0
(D) 6x + 3y ?1 = 0
(E) 6x + 3y ? 5 = 0
Uma homotetia é caracterizada por seu centro O e por sua constante de proporção k.
Devido a homotetia, devemos ter:


Dos dados do exercício, temos que:
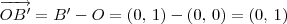

Comparando esses dois vetores, temos que:
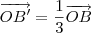
Ou seja, a constante de proporção da homotetia é k=1/3.
Sabendo dessa informação, você pode descobrir quais são as coordenadas do ponto A’.
Em seguida, você pode determinar o coeficiente angular da reta que passa por AA’. Vamos supor que ele seja
m.
Por fim, você pode determinar a reta perpendicular a AA’ e que passa por A’. Lembre-se que o coeficiente angular dessa reta será -1/
m.
Agora tente terminar o exercício.






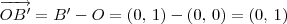

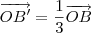
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.