bobkaladao escreveu:Qual é o valor de m para que a área do paralelogramo
determinado pelos vetores u= (0, -3, 1) e v= (1, m, 0) seja
igual a raiz quadrada de 26?Como eu elaboro essa questão? Faço |U x V|=
![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png)
?
Sim, é assim que você deve iniciar.
bobkaladao escreveu:Ou faço o |U x V| e no resultado da matriz eu igualo a
![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png)
?
Quando você diz "resultado da matriz", suponho que você está se referindo ao determinante com o qual você calcularia

. Ou seja, o resultado do determinante:

Note que o resultado desse determinante é um
vetor. Sendo assim, não faz sentido igualá-lo ao
escalar 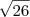
.
Por outro lado, ao calcular o
módulo de um vetor obtemos um escalar. Dessa forma, faz sentido escrever
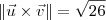
.
Em resumo:

é um vetor;

é um escalar.
bobkaladao escreveu:E mais um favor, se conhecerem algum bom material sobre vetores que possam me indicar eu agradeceria muito, pois estou meio perdido nesta matéria.
Eu recomendo o livro "Matrizes, Vetores e Geometria Analítica" de Reginaldo J. Santos. Ele está disponível na página pessoal de Santos:
Reginaldo J. Santoshttp://www.mat.ufmg.br/~regi/Além desse livro, eu também recomendo:
- Reis, Genésio; Silva, Valdir. Geometria Analítica. 2ª Edição. Rio de Janeiro: Editora LTC, 1996.
- Boulo, Paulo; Camargo, Ivan de. Geometria analítica: um tratamento vetorial. 3ª Edição. São Paulo: Pearson Prentice Hall, 2005.
![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png) ?
?![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png) ?
?

 . Ou seja, o resultado do determinante:
. Ou seja, o resultado do determinante:
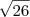 .
.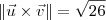 .
. é um escalar.
é um escalar.
