 por geo_nascimento » Dom Out 23, 2011 15:47
por geo_nascimento » Dom Out 23, 2011 15:47
Boa tarde,
não consigo realizar umas questões de elipse e hipérbole ela tem cara de fácil mas pra mim é uma pedra no sapato:
Determinar a equação da elipse de centro C(0,0), focos no eixo de x, excentricidade e=2/3 e passa pelo ponto P(2,-5/3). Não sei por onde começar...
E tem essa também que tá dando uma dor de cabeça : Determine o centro, focos, semi-eixos, assíntota e reta diretriz (se houver) da equação 9x²-58y²+18y+29=0.
por favor me ajudem, tenho um teste sobre isso, obrigado!
-
geo_nascimento
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Out 23, 2011 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Seg Out 24, 2011 16:33
por LuizAquino » Seg Out 24, 2011 16:33
geo_nascimento escreveu:não consigo realizar umas questões de elipse e hipérbole ela tem cara de fácil mas pra mim é uma pedra no sapato:
De fato, as duas questões são fáceis como você verá a seguir. É só trabalhar com as definições e características das cônicas.
Determinar a equação da elipse de centro C(0,0), focos no eixo de x, excentricidade e=2/3 e passa pelo ponto P(2,-5/3).
A equação dessa elipse tem o formato:

, sendo
a e
b números positivos e não nulos.
Por
definição, sabemos que sua excentricidade é dada pela relação:
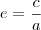
, sendo que
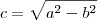
e
a >
b .
Sendo assim, dos dados do exercício temos a equação:

O outro dado do exercício diz que a elipse passa pelo ponto (2, -5/3). Isso significa que esse ponto deve atender a equação da elipse. Isto é, podemos escrever que:

Considerando então as duas equações que foram obtidas, para resolver o exercício basta calcular a solução do sistema:
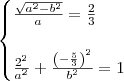
Agora tente terminar a resolução.
Determine o centro, focos, semi-eixos, assíntota e reta diretriz (se houver) da equação 9x²-58y²+18y+29=0.
Será necessário arrumar a equação para que ele fique no formato reduzido. Para isso, nesse caso deve-se completar quadrados em relação a variável
y.

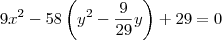
![9x^2 - 58\left[\left(y - \frac{9}{58}\right)^2 - \left(\frac{9}{58}\right)^2\right] + 29=0 9x^2 - 58\left[\left(y - \frac{9}{58}\right)^2 - \left(\frac{9}{58}\right)^2\right] + 29=0](/latexrender/pictures/bdb47d559860881f982236c706216f7c.png)

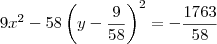
Dividindo toda essa equação por
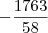
:

Note que essa equação representa uma hipérbole.
Agora tente identificar as características solicitadas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificuldade em exercícios de demonstração
por lipelfnc » Ter Jan 24, 2012 14:34
- 3 Respostas
- 2855 Exibições
- Última mensagem por fraol

Ter Jan 24, 2012 19:15
Cálculo: Limites, Derivadas e Integrais
-
- Dificuldade em exercícios de demonstração
por lipelfnc » Qua Jan 25, 2012 20:16
- 3 Respostas
- 2241 Exibições
- Última mensagem por LuizAquino

Qua Jan 25, 2012 22:46
Cálculo: Limites, Derivadas e Integrais
-
- Essa elipse e essa parábola se encontram?
por Gregorio Diniz » Qua Mar 12, 2014 17:00
- 2 Respostas
- 1843 Exibições
- Última mensagem por Gregorio Diniz

Qua Mar 12, 2014 18:32
Geometria Analítica
-
- [HIPÉRBOLE] Porque yz = 4 é uma hipérbole??
por Sohrab » Qui Abr 25, 2013 03:41
- 1 Respostas
- 2696 Exibições
- Última mensagem por LuizAquino

Qui Abr 25, 2013 19:17
Geometria Analítica
-
- [Parábola]Determinar vértice de parábola (Urgente!)
por migvas99 » Seg Out 08, 2012 14:37
- 1 Respostas
- 2849 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 17:09
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , sendo
, sendo 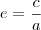 , sendo que
, sendo que 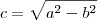 e
e 

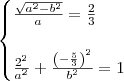

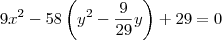
![9x^2 - 58\left[\left(y - \frac{9}{58}\right)^2 - \left(\frac{9}{58}\right)^2\right] + 29=0 9x^2 - 58\left[\left(y - \frac{9}{58}\right)^2 - \left(\frac{9}{58}\right)^2\right] + 29=0](/latexrender/pictures/bdb47d559860881f982236c706216f7c.png)

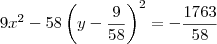
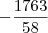 :
:






