por Cristiano Tavares » Dom Set 04, 2011 12:41
por Cristiano Tavares » Dom Set 04, 2011 12:41
Olá a todos,
Não estou conseguindo resolver uma questão sobre cônicas. Nessa questão são dados cinco pontos que pertencem à cônica: P(1,1), Q(2,1), R(3,-1), S(-3,2) e T(-2,-1). Pergunta-se então qual é a equação da cônica.
Sei que a forma geral da equação de uma cônica (parábola, elipse, hipérbole) é Ax² + Bxy + Cy² + Dx + Ey + F = 0. Sei também que os pontos dados acima devem ser substituídos nessa equação geral, encontrando-se então um sistema de cinco equações com as incógnitas A, B, C, D, E, e F. O problema é que não estou conseguindo resolver esse sistema, não estou entendendo o fato de serem seis variáveis e apenas cinco equações.
Alguém poderia me ajudar a resolver esse sistema de equações?
-
Cristiano Tavares
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Mai 11, 2011 21:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
 por LuizAquino » Dom Set 04, 2011 20:11
por LuizAquino » Dom Set 04, 2011 20:11
Como você mesmo escreveu, a equação geral da cônica é:

Entretanto, tem um detalhe: por definição temos que A, B ou C deve ser diferente de zero.
Suponha que A é diferente de zero. Veja que você pode fazer:
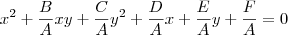
Agora façamos
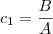
,
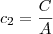
,

,

e

. A equação pode então ser escrita como:
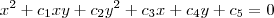
Veja que dados os cinco pontos, você pode determinar as cinco constantes acima.
Por outro lado, veja que se A fosse zero, então B ou C não seria. Bastava então dividir toda a equação pela constante que não fosse nula. Novamente você poderia criar cinco novas constantes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sobre as Cônicas
por Jhenrique » Seg Dez 10, 2012 18:51
- 4 Respostas
- 3063 Exibições
- Última mensagem por Jhenrique

Seg Dez 17, 2012 21:35
Geometria Analítica
-
- Geometria Analítica [Dúvida] sobre cônicas
por pablohas » Sáb Dez 04, 2010 12:55
- 6 Respostas
- 5707 Exibições
- Última mensagem por pablohas

Seg Dez 06, 2010 20:17
Geometria Analítica
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1523 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
-
- Questão sobre PA e PG
por Carolziiinhaaah » Qua Jun 16, 2010 17:35
- 5 Respostas
- 5090 Exibições
- Última mensagem por Carolziiinhaaah

Qui Jun 17, 2010 13:31
Progressões
-
- Questão sobre palíndromos!
por mariasse » Sex Jul 09, 2010 16:13
- 2 Respostas
- 3325 Exibições
- Última mensagem por mariasse

Sáb Jul 10, 2010 19:14
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



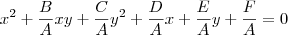
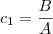 ,
, 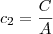 ,
,  ,
,  e
e  . A equação pode então ser escrita como:
. A equação pode então ser escrita como: