-civil- escreveu:Boulos - 3ª ed. - Cap. 18
18-5) Obtenha, em cada caso, uma equação vetorial da reta que contém P, é paralela ou contida no plano

e é concorrente com a reta r.
b) P = (1,0,1);

: x - 3y - z = 1; r: X = (0,0,0) +

(2,1,-1)
Verifiquei que P não pertece a

e que r é paralelo a

. E agora, como encontrar o plano formado entre P e r?
No próprio livro citado, há a seguinte proposição:
r e s são concorrentes se e somente se são coplanares e não são paralelas. Ou seja, se e somente se:
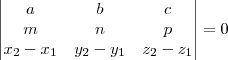
,
e
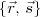
é L. I., sendo que
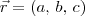
vetor diretor de r,
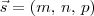
vetor diretor de s,
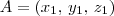
um ponto de r e
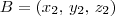
um ponto de s.
Note que pelos dados do exercício você pode obter o vetor

, um ponto A de r e um ponto B de s. Fica faltando
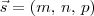
.
Além disso, perceba que como r e s são concorrentes e paralelas ao plano

, podemos tomar
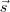
de tal modo que
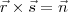
, sendo

o vetor normal de

.
Unindo essa última informação com o determinante acima, você monta um sistema linear com três incógnitas (m, n e p) e duas equações. A partir disso você obtém
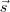
.
-civil- escreveu:d) P = (2,-1,2);

: x + y +z = 0; r é a intersecção dos planos
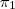
: x=z e

: z = y + 2
Verifiquei que P não pertence a

e também não pertence a r. Mas como prosseguir?
Note que r é perpendicular ao plano

. Para s ser paralela a

e concorrente a r, deve existir um ponto Q de r tal que

e
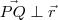
. Após determinar esse ponto Q, basta tomar o vetor diretor de s como sendo
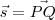
.
 e é concorrente com a reta r.
e é concorrente com a reta r. : x - 3y - z = 1; r: X = (0,0,0) +
: x - 3y - z = 1; r: X = (0,0,0) +  (2,1,-1)
(2,1,-1) e que r é paralelo a
e que r é paralelo a  . E agora, como encontrar o plano formado entre P e r?
. E agora, como encontrar o plano formado entre P e r? : x + y +z = 0; r é a intersecção dos planos
: x + y +z = 0; r é a intersecção dos planos  1: x=z e
1: x=z e  2: z = y + 2
2: z = y + 2 e também não pertence a r. Mas como prosseguir?
e também não pertence a r. Mas como prosseguir?

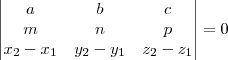 ,
, 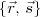 é L. I., sendo que
é L. I., sendo que 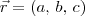 vetor diretor de r,
vetor diretor de r, 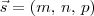 vetor diretor de s,
vetor diretor de s, 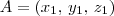 um ponto de r e
um ponto de r e 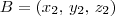 um ponto de s.
um ponto de s. , um ponto A de r e um ponto B de s. Fica faltando
, um ponto A de r e um ponto B de s. Fica faltando 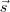 de tal modo que
de tal modo que 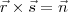 , sendo
, sendo  o vetor normal de
o vetor normal de 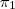 : x=z e
: x=z e  : z = y + 2
: z = y + 2 e
e 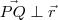 . Após determinar esse ponto Q, basta tomar o vetor diretor de s como sendo
. Após determinar esse ponto Q, basta tomar o vetor diretor de s como sendo 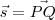 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.