 por 0 kelvin » Qui Mar 24, 2011 20:35
por 0 kelvin » Qui Mar 24, 2011 20:35
Justifiquei usando a definição que esta no livro do P. Boulos e Camargo. Se o vetor não é nulo, o comprimento dele é maior que 0, portanto, a afirmação ||

|| > 0 é verdadeira. ||
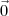
|| > 0 não existe.
É assim que prova?
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por MarceloFantini » Qui Mar 24, 2011 20:51
por MarceloFantini » Qui Mar 24, 2011 20:51
Bom, normalmente eu faço assim: tomando

, com

, temos que

. Como

(pois são diferentes de zero), segue que

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por 0 kelvin » Qui Mar 24, 2011 21:16
por 0 kelvin » Qui Mar 24, 2011 21:16
Uhm.. reparei que tem uma diferença entre a segunda a terceira edição do livro. Na segunda tem a definição do vetor e daí vem as operações. Na terceira tem uma lista de definições e até uma parte de analogia pra explicar o conceito, antes de começarem as operações. Como eu vi o exercicio na terceira edição que tinha na biblioteca, não tinha reparado que fizeram essa mudança de uma edição pra outra, daí nem vi as operações antes do exercicio. Esse exercicio nem tem na segunda edição

Os textos tambem foram bastante revisados, na terceira edição tinha um aviso "cuidado com a expressão vetores equipontes", que não tem na segunda.
Tomando a definição do
segmento orientado, entendi a prova por Pitágoras.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Provar se é par
por stalone » Seg Dez 21, 2009 23:29
- 5 Respostas
- 3221 Exibições
- Última mensagem por stalone

Seg Dez 13, 2010 13:07
Desafios Difíceis
-
- Provar
por scggomes » Sex Abr 15, 2011 16:38
- 8 Respostas
- 5948 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 16, 2011 15:56
Cálculo para Funções de Uma Variável Real I
-
- provar que
por anamendes » Ter Jun 19, 2012 07:41
- 1 Respostas
- 1423 Exibições
- Última mensagem por fraol

Qua Jun 20, 2012 21:19
Trigonometria
-
- Provar
por Jovani Souza » Ter Jun 11, 2013 21:03
- 0 Respostas
- 1020 Exibições
- Última mensagem por Jovani Souza

Ter Jun 11, 2013 21:03
Álgebra Elementar
-
- provar!
por Jovani Souza » Qua Jul 03, 2013 18:27
- 0 Respostas
- 1177 Exibições
- Última mensagem por Jovani Souza

Qua Jul 03, 2013 18:27
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 || > 0 é verdadeira. ||
|| > 0 é verdadeira. ||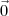 || > 0 não existe.
|| > 0 não existe.
 || > 0 é verdadeira. ||
|| > 0 é verdadeira. ||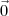 || > 0 não existe.
|| > 0 não existe.
 , com
, com  , temos que
, temos que  . Como
. Como  (pois são diferentes de zero), segue que
(pois são diferentes de zero), segue que  .
.



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
