geriane escreveu:Em uma cabine de um estádio de futebol, um computador registra todos os lances de uma partida. Em um desses lances, Zaqueu cobrou uma falta, fazendo a bola descrever um arco de parábola contido num plano vertical, parábola esta simétrica ao seu eixo, o qual também era vertical. A bola caiu no chão exatamente a 30m de Zaqueu. Durante o trajeto, a bola passou raspando a cabeça do juiz. O juiz, que não interferiu na trajetória da bola, tinha 1,76m de altura e estava ereto, a 8m de distância de onde saiu o chute. Desse modo, a altura máxima, em metros, atingida pela bola foi de:
a) 2,25m b) 4,13m c) 6,37m d) 9,21m e) 15,92m
Boa tarde.
Primeiramente desenhe uma parábola onde as raízes (que cortam o eixo x) serão 0 e 30, pois é de onde a bola parte e onde ela chega. Essa parábola será côncava para baixo, já que é assim que a bola percorre sua trajetória e tem essa cara:
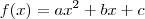
.
Temos então que quando

,

.


Então a função terá essa cara:

Agora vamos usar a informação dos pontos que temos. Quando

,

.
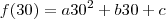
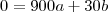
 (equação 1)
(equação 1)Outra informação do gráfico que temos é a posição do juiz. Quando

,

.
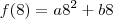
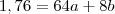 (equação 2)
(equação 2)Substituindo a equação 1 na equação 2 você encontrará

.
(o que garante a concavidade para baixo).
Com o valor de a você substitui na equação 1 e encontra

Ou seja, a equação tem essa cara:
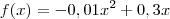
Como ele quer saber a altura máxima e a equação é simétrica, basta calcular y no ponto de
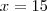
(já que é a metade de 30).
Calculando o

chegamos em
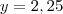
, que é a altura máxima.
Qualquer dúvida, informe!



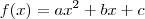 .
. ,
,  .
.


 ,
, 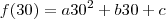
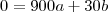

 ,
,  .
.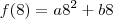
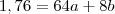
 .
.
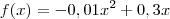
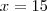 (já que é a metade de 30).
(já que é a metade de 30). chegamos em
chegamos em 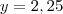 , que é a altura máxima.
, que é a altura máxima.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
