 por Anna_lu » Seg Mar 23, 2015 14:23
por Anna_lu » Seg Mar 23, 2015 14:23
Olá! Eu estou com dúvida não na resolução do seguinte exercício, mas na interpretação dele. o enunciado é:
Se {
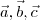
} é uma base ortonormal e
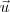
, um vetor qualquer, então
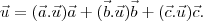
.
a resolução dele : O que sabemos é que
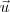
pode ser escrito de maneira única como uma combinação linear de
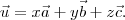
. Calculando, então, o produto interno
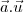
, obtemos
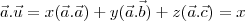
.
A minha dúvida é a seguinte, por que a expressão :
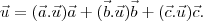
. multiplica por
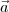
( após ao primeiro parênteses) , por
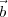
( após o segundo parênteses) e por
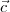
( após ao terceiro parênteses)?
Obrigada,
-
Anna_lu
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Mar 23, 2015 12:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Seg Mar 23, 2015 19:33
por adauto martins » Seg Mar 23, 2015 19:33
uma base {a,b,c} eh ortonormal,qdo os vetores sao unitarios e mutuamente pérpndiculares,ou seja:
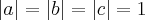
e
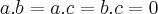
...
entao seja u um vetor no espaço gerado por {a,b,c}...
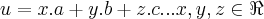
...logo...
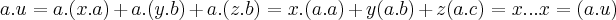
...de modo analogo teremos p/b.u e c.u...
assim...u=(a.u).a+(b.u).b+(c.u).c...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Bases e dimensões] exercício rápido
por GuilhermeOliveira » Dom Jun 24, 2012 23:12
- 3 Respostas
- 2226 Exibições
- Última mensagem por GuilhermeOliveira

Seg Jun 25, 2012 13:08
Geometria Analítica
-
- Dimensoes e bases em R3
por ThunderHawk » Dom Mar 15, 2009 08:09
- 0 Respostas
- 1866 Exibições
- Última mensagem por ThunderHawk

Dom Mar 15, 2009 08:09
Álgebra Elementar
-
- Bases numéricas
por jann lucca » Seg Jun 18, 2012 17:04
- 1 Respostas
- 1872 Exibições
- Última mensagem por Guill

Sáb Jun 30, 2012 18:13
Álgebra Elementar
-
- Tranfomação de bases
por Pedro Miguel » Qua Abr 23, 2014 01:04
- 0 Respostas
- 1110 Exibições
- Última mensagem por Pedro Miguel

Qua Abr 23, 2014 01:04
Aritmética
-
- [Bases e subespaços] qual a diferença ?
por GuilhermeOliveira » Seg Jun 25, 2012 13:34
- 2 Respostas
- 1552 Exibições
- Última mensagem por GuilhermeOliveira

Seg Jun 25, 2012 17:23
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
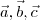 } é uma base ortonormal e
} é uma base ortonormal e 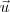 , um vetor qualquer, então
, um vetor qualquer, então 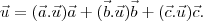 .
. 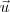 pode ser escrito de maneira única como uma combinação linear de
pode ser escrito de maneira única como uma combinação linear de 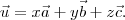 . Calculando, então, o produto interno
. Calculando, então, o produto interno 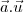 , obtemos
, obtemos 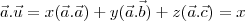 .
. 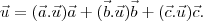 . multiplica por
. multiplica por 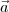 ( após ao primeiro parênteses) , por
( após ao primeiro parênteses) , por 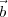 ( após o segundo parênteses) e por
( após o segundo parênteses) e por 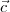 ( após ao terceiro parênteses)?
( após ao terceiro parênteses)?

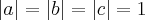 e
e 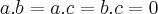 ...
...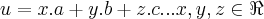 ...logo...
...logo...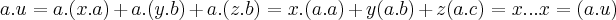 ...de modo analogo teremos p/b.u e c.u...
...de modo analogo teremos p/b.u e c.u...