Olá. Não estou conseguindo entender um exercício sobre vetores. O exercício diz o seguinte: "Prove que, se o vetor u é um múltiplo escalar do vetor v (u=k.v), então qualquer sequência que contém os vetores u e v é linearmente dependente (LD)". Bom, o meu raciocínio ficou assim: temos, por hipótese, que o vetor u é um múltiplo escalar do vetor v e, portanto, são paralelos e, logo, a sequência de vetores (u,v) é linearmente dependente (LD). Agora, temos que pensar no caso de uma sequência de três vetores e no caso com quatro ou mais vetores. Neste último, com quatro ou mais, por definição, sabemos que tal sequência é sempre linearmente dependente. Agora, o que eu não consigo entender é o caso de três vetores numa sequência. Teríamos que pensar numa sequência com, é claro, os vetores u e v, e acrescentar mais um, por exemplo, um vetor w. Assim, seria uma sequência (u, v, w) para provar que é LD. Porém, pelo que estudei, entendo que uma sequência com três vetores é LD quando todos os vetores em questão são paralelos à um mesmo plano; e são LI (linearmente independente) quando ocorre o contrário, se, por exemplo, o vetor w é não é paralelo ao mesmo plano que os outros dois vetores são. Sei também que existe uma proposição tal que diz que a sequência de vetores (u, v, w) é LD se, e somente se, um dos vetores é gerado pelos outros dois, no caso, w gerado por u e v. Eu acho que o certo é usar esta proposição para provar que a sequência é LD. Procurei saber como usar tal proposição e me disseram que devo usar o coeficiente igual a zero multiplicando o vetor w, mas eu não consigo entender como podemos simplesmente acrescentar o zero assim! (Parece uma questão boba, mas não entendo).
Obrigada!
vetores sobre um espaço vetorial 
onde por simplicidade trocamos 
por 
e 
por 
vamos mostra que se (u_1,u_2 ) L.D. então a sequência ou n-upla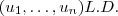 
. Suponhamos inicialmente que tenhamos uma combinação linear nula , 
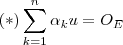(em que
é o vetor nulo do espaço vetorial E ) . 
, reescrevendo 
(
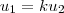) temos :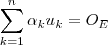
sse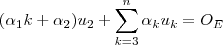 
. Se os vetores 
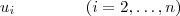são L.D. obteremos escalares não todos nulos satisfazendo 
chegando a conclusão que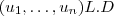 
,caso eles são L.I. resulta , 
. 
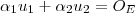, desde que por hipótese 
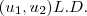esta combinação linear nula admite solução além da trivial . Assim obtemos escalares 
não todos nulos tais que ,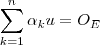 
e portanto 
. 
ou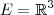 
ou generalizar 
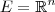. Mas em geral para espaços abstratos vale a solução (acredito ) .
por