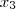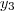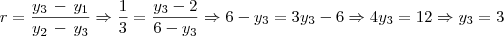por GABRIELA » Ter Out 20, 2009 16:28
por GABRIELA » Ter Out 20, 2009 16:28
As coordenadas de um ponto P, que divide o segmento AB,onde A (3,2) B (-1,6), na razão

é?
Alguém poderia me ajudar a resolver essa questão?
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por thadeu » Qua Out 21, 2009 12:12
por thadeu » Qua Out 21, 2009 12:12
Basta você usar as coordenadas do ponto divisor usando razão de secção:
Temos os pontos

, calcularemos as coordenadas do ponto

que divide o segmento

na razão

Calculando a coordenada
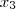

Fazendo a mesma coisa para encontar a coordenada
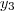
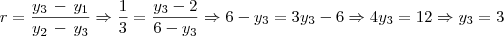
As coordenadas são

-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12985 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- AJUDA NA QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:00
- 1 Respostas
- 1447 Exibições
- Última mensagem por Molina

Ter Set 08, 2009 18:58
Matrizes e Determinantes
-
- Ajuda em questão
por Igor » Sex Dez 03, 2010 19:20
- 2 Respostas
- 1381 Exibições
- Última mensagem por Lorettto

Sáb Dez 04, 2010 19:24
Polinômios
-
- Ajuda - Questão FCC
por cesilva » Qui Jan 31, 2013 12:36
- 2 Respostas
- 2672 Exibições
- Última mensagem por cesilva

Qui Jan 31, 2013 16:14
Lógica
-
- Ajuda na questão de Pré-Cálculo
por Jamilly » Ter Mar 16, 2010 10:12
- 5 Respostas
- 4344 Exibições
- Última mensagem por Jamilly

Qua Mar 17, 2010 20:24
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é?
é?
 é?
é?
 , calcularemos as coordenadas do ponto
, calcularemos as coordenadas do ponto  que divide o segmento
que divide o segmento  na razão
na razão