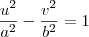Sohrab escreveu:Pessoal, estou estudando quádricas e cilindros..
Uma questão pede para descrever e esboçar o gráfico de uma superfície
yz = 4
eu vi nas repostas, e é uma hipérbole (um cilindro hiperbólico, na verdade, já que o traço dessa hipérbole se repete para cada valor de x (cilindro paralelo ao eixo x))
mas não estou conseguindo entender porque, as interseções de yz = 4 com os planos x = k(constante) dão hipérbole no plano yz.. desde quando isso é uma equação de hipérbole?
por exemplo.. como vou achar os focos, centro, etc dessa hipérbole?
O seu problema é que você está querendo uma equação da hipérbole no formato padrão, ou seja, algo do tipo:
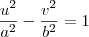
Mas acontece que se uma hipérbole está rotacionada em relação ao sistema de coordenadas, então aparecerá em sua equação um termo misto (ou termo cruzado), isto é, um termo do tipo uv. Para eliminar este termo, você precisa efetuar uma rotação de eixos, de modo que no novo sistema a hipérbole não esteja mais rotacionada.
Eu gostaria de sugerir que você assista a videoaula "33. Geometria Analítica - Rotação de Eixos". Eu espero que ela possa lhe ajudar a entender melhor o problema. Esta videoaula está disponível no curso de Geometria Analítica em minha página:
http://www.lcmaquino.org/