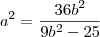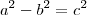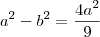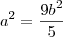por MrJuniorFerr » Qua Out 31, 2012 12:58
por MrJuniorFerr » Qua Out 31, 2012 12:58
Pessoal to com dúvida no seguinte exercício:
Determinar a equação da elipse que satisfaz as condições dadas:
centro  , focos no eixo dos x, excentricidade
, focos no eixo dos x, excentricidade 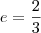 e passa pelo ponto
e passa pelo ponto 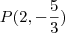 .
.Bom, sei que

, portanto

, então,
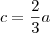
Em relação ao ponto dado, tentei substitui-lo em x e y na fórmula da elipse

, e tirando o mmc, e isolando o

, obtive
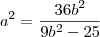
Como fazer esse exercício?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cônicas - Elipse - Só uma dúvida simples
por samra » Sex Jan 24, 2014 01:39
- 2 Respostas
- 1679 Exibições
- Última mensagem por samra

Sex Jan 24, 2014 19:21
Geometria Analítica
-
- (CÕNICAS) Elipse
por manuel_pato1 » Sex Nov 23, 2012 01:04
- 4 Respostas
- 2355 Exibições
- Última mensagem por manuel_pato1

Sex Nov 23, 2012 14:42
Geometria Analítica
-
- (CONICAS) equação da elipse
por manuel_pato1 » Sáb Nov 17, 2012 20:53
- 4 Respostas
- 2837 Exibições
- Última mensagem por manuel_pato1

Qua Nov 21, 2012 20:44
Geometria Analítica
-
- Cônicas: Elipse, me ajudem, por favor!
por felipe_08 » Qui Mai 28, 2015 22:48
- 0 Respostas
- 1197 Exibições
- Última mensagem por felipe_08

Qui Mai 28, 2015 22:48
Geometria Analítica
-
- [Cônicas] duvida.
por Fabricio dalla » Qui Dez 01, 2011 12:32
- 5 Respostas
- 3864 Exibições
- Última mensagem por TheoFerraz

Sex Dez 09, 2011 16:01
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , focos no eixo dos x, excentricidade
, focos no eixo dos x, excentricidade 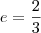 e passa pelo ponto
e passa pelo ponto 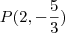 .
. , portanto
, portanto  , então,
, então, 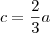
 , e tirando o mmc, e isolando o
, e tirando o mmc, e isolando o  , obtive
, obtive