Seja

, cujo coeficiente angular é

, e
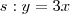
, cujo coeficiente angular é

.
Da interpretação geométrica do coeficiente angular, podemos calcular o ângulo agudo

formado pelas retas:
Como

, decorre que

, isto é,

é o ângulo que a reta

faz com a reta

, portanto, com o eixo
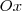
já que, de fato, a reta

é o próprio eixo das abicissas.
Queremos a equação da bissetirz interna do ângulo

. Note que o coeficiente linear da reta supracitada será nulo, já que a mesma também passa pela origem assim como as demais retas em questão. Além disso o ângulo que a reta bissetriz forma com o eixo
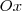
é

, em decorrência da definição de bissetriz.
Concluímos assim, que o coeficiente angular da reta bissetriz será numericamente igual a:

Usando a relação de duplicação do arco para a função tangente, temos:

Chamando
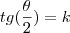
, como

, temos:
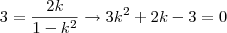
e decorre em,
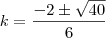
, e como esse valor deve ser positivo pois o ângulo pertence ao primeiro quadrante,
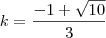
, que é o coeficiente angular da bissetriz.
Assim, a equação da reta bissetriz é:

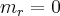
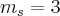


 , cujo coeficiente angular é
, cujo coeficiente angular é  , e
, e 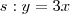 , cujo coeficiente angular é
, cujo coeficiente angular é  .
. formado pelas retas:
formado pelas retas: , isto é,
, isto é,  faz com a reta
faz com a reta  , portanto, com o eixo
, portanto, com o eixo 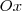 já que, de fato, a reta
já que, de fato, a reta  é o próprio eixo das abicissas.
é o próprio eixo das abicissas. , em decorrência da definição de bissetriz.
, em decorrência da definição de bissetriz.

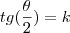 , como
, como  , temos:
, temos: 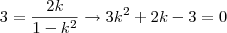 e decorre em,
e decorre em, 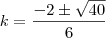 , e como esse valor deve ser positivo pois o ângulo pertence ao primeiro quadrante,
, e como esse valor deve ser positivo pois o ângulo pertence ao primeiro quadrante, 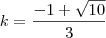 , que é o coeficiente angular da bissetriz.
, que é o coeficiente angular da bissetriz.



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.