Se
 e
e ![B(-5,3.\sqrt[]{3}) B(-5,3.\sqrt[]{3})](/latexrender/pictures/d9d43e65040405a6b8e76bc2e7277819.png) são pontos de uma elipse cujos focos são
são pontos de uma elipse cujos focos são  e
e 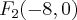 , calcule a área do triângulo
, calcule a área do triângulo  .
.Apresentando minha resolução:

Gostaria de saber se alguém pode apresentar algum outro modo de resolução, e fazer o desenho da elipse.
Até mais.

 e
e ![B(-5,3.\sqrt[]{3}) B(-5,3.\sqrt[]{3})](/latexrender/pictures/d9d43e65040405a6b8e76bc2e7277819.png) são pontos de uma elipse cujos focos são
são pontos de uma elipse cujos focos são  e
e 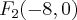 , calcule a área do triângulo
, calcule a área do triângulo  .
.

 (distancia entre os focos) e a altura é
(distancia entre os focos) e a altura é  :
: 
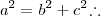





Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)