 por Emanuel » Sáb Abr 03, 2010 10:12
por Emanuel » Sáb Abr 03, 2010 10:12
Pessoal tenho dificuldades, não sei resolver, preciso entregar um trabalho na dia 6/04/10. preciso muito de sua ajuda, tenho varios exercicios q não consegui resolver. se puderem me ajudar.
1 - Calcule a diagonal, a area total e o volume de um cubo de aresta igual a 5 cm.
2 - A altura de um prisma triangular regular é 10cm. Calcule a área lateral, a area total e o volume desse prisma sabendo-se que a aresta da base mede 6cm.
3 - um poliedro convexo possui 5 faces triangulares, 4 faces quadrangulares e 3 faces pentagonais. Quantos vertices, possui esse poliedro?
4 - Determine a área do hexagono de lado 8 cm.
por favor, me ajudem. tenho muitos exercicios q não consegui resolver.
desde ja sou grato.
-
Emanuel
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Abr 03, 2010 09:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso técnico em informatica
- Andamento: formado
 por davi_11 » Sáb Abr 03, 2010 12:59
por davi_11 » Sáb Abr 03, 2010 12:59
1. Usando o teorema de pitágoras em uma aresta e a diagona de uma das faces
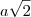
você chega na diagonal do cubo:

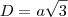
2.Se o prisma é regular, suas bases são triangulos equilateros. A área lateral é a soma das áreas dos quadriláteos laterais

A área total é a área da base somado com as áreas dos dois triângulos equiláteros.
O volume é dado pela área da base multiplicado pela altura.
3.Teorema de Euler: "Em qualquer poliedro convexo, a soma do número de faces com o n° de vértices é igual ao n° de arestas aumentado de duas unidades".
O n° de arestas pode ser dado por:
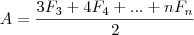
Onde

é o número de faces com n lados.
4.Se o hexagono for regular, a área é dada pela área de um triângulo equilátero de lado igual multiplicado por seis. Se não for esse o caso, você senta e chora.
"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
 por davi_11 » Sáb Abr 03, 2010 13:01
por davi_11 » Sáb Abr 03, 2010 13:01
Obs: Isto não é geometria analítica.

"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
 por Emanuel » Sáb Abr 03, 2010 13:03
por Emanuel » Sáb Abr 03, 2010 13:03
OBs: Mat > > num sei nada!
-
Emanuel
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Abr 03, 2010 09:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso técnico em informatica
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Tenho dificuldades em calcucar Z em diversos casos.
por Leojpa400 » Ter Nov 08, 2011 13:56
- 4 Respostas
- 2407 Exibições
- Última mensagem por Leojpa400

Seg Nov 28, 2011 14:00
Números Complexos
-
- urgente!! tenho prova amanhã!!
por hopiloto » Ter Jul 12, 2011 12:33
- 0 Respostas
- 1162 Exibições
- Última mensagem por hopiloto

Ter Jul 12, 2011 12:33
Sequências
-
- preciso de ajuda urgente!!!!
 por matematicada » Qua Nov 24, 2010 12:17
por matematicada » Qua Nov 24, 2010 12:17
- 2 Respostas
- 2068 Exibições
- Última mensagem por matematicada

Qui Nov 25, 2010 11:39
Funções
-
- preciso de ajuda, é urgente
por nayane » Sex Nov 26, 2010 21:12
- 2 Respostas
- 2025 Exibições
- Última mensagem por nayane

Sáb Nov 27, 2010 14:40
Álgebra Elementar
-
- PRECISO DA RESPOSTA URGENTE
por trix17 » Qua Nov 09, 2011 23:34
- 0 Respostas
- 1394 Exibições
- Última mensagem por trix17

Qua Nov 09, 2011 23:34
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


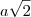 você chega na diagonal do cubo:
você chega na diagonal do cubo:
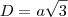

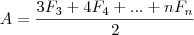
 é o número de faces com n lados.
é o número de faces com n lados.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.