Os vetores,
e
serão linearmente independentes desde que as constantes
sejam ambas diferentes de zero.
Eu comecei a responder levantando as seguintes questões:
1. Sempre serão LI caso a condição "h, k ambas diferentes de zero" seja atendida?
2. Se apenas h ou apenas k for diferente de zero os vetores serão LI?
*Note que se os vetores forem LD mesmo que as constantes h, k sejam ambas diferentes de zero a questão será falsa
Primeiro calculei o determinante, tendo noção de que Det = 0 é LD e Det ? 0 é LI
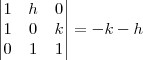
A partir disso notei que se k = h o determinante seria ? 0, logo os vetores seriam LI. Caso k = -h, o determinante seria = 0, e os vetores LD.
Por fim, considerei k = 2, h = -2, tendo:
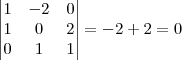
Com isso, conclui que mesmo que h,k sejam ambas diferentes de zero, os vetores não serão sempre LI, caso k = -h eles serão LD. Logo, a questão é FALSA.
Tenho mais duas perguntas acerca desse enunciado:
1) Como resolver essa questão a partir de sistemas? Calculei, mas não consegui concluir muita coisa com
. Só tive a mesma noção ao fazer a combinação linear, considerando a condição que obtive a partir do determinante.2) Existe um método mais rápido de responder questões como essa? Calculei sendo ambas igual a zero, ambas diferentes de zero e apenas uma sendo zero, antes de ter esse raciocínio.
Obrigada!
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.