A sua confusão é bastante natural.
Um sistema de coordenadas é inerte a
definição, assim como 90% das "coisas" da Matemática. Assim,
definimos que o ponto P de coordenadas cartesianas
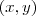
terá, no sistema polar, coordenadas

tais que

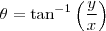
Isso você já sabe. O detalhe é que o ponto
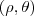
deve corresponder a UM ÚNICO ponto cartesiano
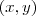
. Isto é, dois pontos diferentes não podem ter o mesmo argumento. Daí, definimos que o argumento é contado do eixo x em direção ao eixo y positivamente de modo que

ou, equivalentemente,
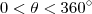
.
O ponto , por exemplo,
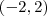
também é tal que
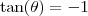
. Mas seu argumento é

pois ele pertence ao 2° quadrante.
O seu ponto pertence ao 4°. Logo, seu argumento deve ser 315°.
Afinal, quantas soluções possui a equação

? Infinitas. Porém, restringidas ao intervalo
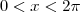
apenas DUAS. Este é o sucesso da coordenação polar: cada ponto no espaço pode ser definido UNIVOCAMENTE, assim como no cartesiano.



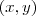 terá, no sistema polar, coordenadas
terá, no sistema polar, coordenadas  tais que
tais que
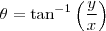
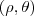 deve corresponder a UM ÚNICO ponto cartesiano
deve corresponder a UM ÚNICO ponto cartesiano  ou, equivalentemente,
ou, equivalentemente, 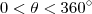 .
.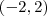 também é tal que
também é tal que 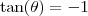 . Mas seu argumento é
. Mas seu argumento é  pois ele pertence ao 2° quadrante.
pois ele pertence ao 2° quadrante. ? Infinitas. Porém, restringidas ao intervalo
? Infinitas. Porém, restringidas ao intervalo 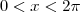 apenas DUAS. Este é o sucesso da coordenação polar: cada ponto no espaço pode ser definido UNIVOCAMENTE, assim como no cartesiano.
apenas DUAS. Este é o sucesso da coordenação polar: cada ponto no espaço pode ser definido UNIVOCAMENTE, assim como no cartesiano.

 .
.
 :
: