Por favor, gostaria de ajuda com este exercícios:
1) Descreva o conjunto dos vetores w que são ortogonais a v=(2,1,2) e que u=(1,1,-1) seja combinação linear de v e w.
Eu tentei resolver desse jeito:
Sejam S={v1,v2,v3} Então S={(a,b,c),(2,1,2),(1,1,-1)}
Logo:
v1.v3=(a,b,c).(1,1,-1)=a+b-c=0
v1.v2=(a,b,c).(2,1,2)=2a+b+2c=0
v1.v3=(2,1,2).(1,1,-1)=2+1-2=0
a+b-c=0
2a+b+2c=0
2+1-2=0
Só consegui ir até aí ...


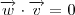 .
.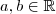 tais que
tais que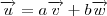 .
.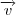 somos capazes de calcular
somos capazes de calcular  .Note que
.Note que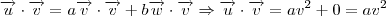
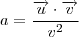 .
. 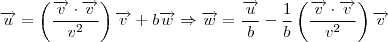
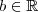 . Daí, podemos tomar
. Daí, podemos tomar 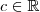 tal que
tal que 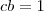 e descrever o conjunto como
e descrever o conjunto como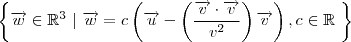


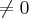
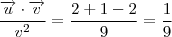 .
.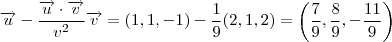 .
.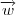 é múltiplo de
é múltiplo de 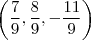 e
e 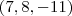 , então
, então![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)