Flordelis,
Flordelis25 escreveu:1)Dada a reta r de equação 2x - 3y + 1 = 0
a) dizer qual a abscissa do ponto de ordenada 3 pertencente à reta r.
Consideremos o ponto

;
- o número dois pertence ao eixo x, portanto,
ABSCISSA;
- o número três pertence ao eixo y, daí,
ORDENADA.
O enunciado fornece a seguinte informação:

. Resta-nos substituir aquele valor na equação da reta
r e encontrar o valor de 'x' (abscissa). Segue,
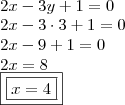
Flordelis25 escreveu:b) determinar os pontos de intersecção da reta r com os eixos coordenados.
Eixos coordenados, a grosso modo, é aquele em que um dos eixos (horizontal ou vertical) é nulo. Tomemos com exemplo o seguinte ponto

, note que o ponto é marcado sobre o eixo vertical (horizontal nulo).
Daí, os eixos coordenados são dados por
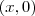
e
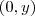
. Segue,
- intersecção do ponto
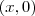
com a reta
r:
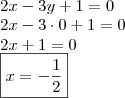
- intersecção do ponto
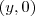
com a reta
r:
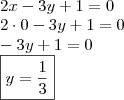
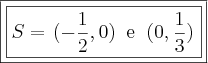
Flordelis25 escreveu:c) determinar o ponto de intersecção da reta r com a reta s, cuja equação é x + y - 1 = 0.
Para resolver essa alínea, deverás isolar o

nas duas equações e igualar. Após encontrar um valor para a abscissa, ou seja, o valor de

, substitua-o em uma das equações da reta para obter o valor de

. Pronto! encontraste o ponto de intersecção.
Espero ter ajudado!
Qualquer dúvida comente!
Att,
Daniel Ferreira.




 ;
; . Resta-nos substituir aquele valor na equação da reta
. Resta-nos substituir aquele valor na equação da reta 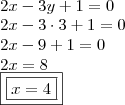
 , note que o ponto é marcado sobre o eixo vertical (horizontal nulo).
, note que o ponto é marcado sobre o eixo vertical (horizontal nulo).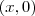 e
e 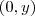 . Segue,
. Segue,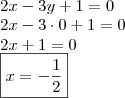
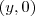 com a reta
com a reta 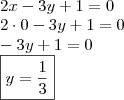
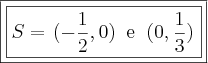
 nas duas equações e igualar. Após encontrar um valor para a abscissa, ou seja, o valor de
nas duas equações e igualar. Após encontrar um valor para a abscissa, ou seja, o valor de  , substitua-o em uma das equações da reta para obter o valor de
, substitua-o em uma das equações da reta para obter o valor de 
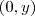 , não é?!
, não é?!

 , avisa que eu resolvo.
, avisa que eu resolvo.

