Escreva uma equação vetorial da reta r concorrente com s, paralela ao plano pi, e perpendicular a reta AB. São dados pi: 2x-y+3z-1=0, A=(1,0,1), B=(0,1,2), s: X=(4,5,0)+a(3,6,1)
Não consigo resolver esse exercício, eu sei de algumas coisas:
Se r é paralela ao plano pi, ela é ortogonal ao vetor (2,-1,3), que é o vetor normal ao plano pi. Logo o produto escalar de r com (2,-1,3) sendo r o vetor diretor de r tem que ser nulo.
Se r é perpendicular a reta AB, então r.(-1,1,1)=0 (o produto escalar do vetor diretor da reta r com o vetor AB tem que ser nulo.)
Mas se eu escrevo a reta r na forma: X=(a,b,c)+y(m,n,p), eu tenho 7 incognitas nessa equação, e mesmo resolvendo os sistemas anteriores ainda me sobrariam varias, não sei bem como posso usar as informações de que r é concorrente com r e perpendicular a reta AB. (Eu acredito que tenho que encontrar os pontos onde as retas se interceptam, mas não sei como isso vai me ajudar, já que eu adicionaria varios parametros das outras retas ao sistema).
Por favor, podem me ajudar a prosseguir com a resolução?
Obrigado.


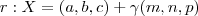 .
.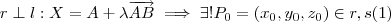 e
e 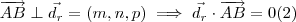 .
.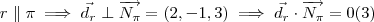 . Por
. Por 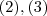 teremos um sistema de três incógnitas para 2 equações ,poderemos por exemplo escrever
teremos um sistema de três incógnitas para 2 equações ,poderemos por exemplo escrever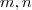 em função de
em função de  .Assim , o conjunto dos vetores múltiplos de
.Assim , o conjunto dos vetores múltiplos de  ,portanto a escolha para
,portanto a escolha para  são concorrentes,então ambas retas possuem um único ponto em comum (4) .Suponha que
são concorrentes,então ambas retas possuem um único ponto em comum (4) .Suponha que 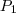 seja este ponto .Tente utilizar (4) e (1) para concluir .Comente as dúvidas .
seja este ponto .Tente utilizar (4) e (1) para concluir .Comente as dúvidas .
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)