Após determinar a interseção entre os planos que designa a reta

.Considere

,respectivamente, vetor diretor da reta

,ponto arbitrário pertencente à reta

,um ponto particular da reta

que satisfaz

(poderemos ter mais de um) e
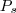
ponto da reta

mais próximo de

tal que
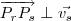
.
Faça um desenho representando ambas retas .Note que,
a)

tal que

.
b)
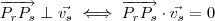
.
c) O vetor
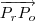
é combinação linear de

.
Pelo item c) ,usando-se o item a) e multiplicando-se escalarmente ambos membos por
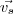
segue-se que :

que devido ao item b) ,resulta :
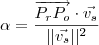
. Aplicando este resultado no item a) ,obtemos :
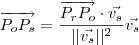
.
Este último resultado implica
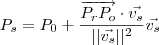
.
O ponto
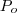
é arbitrário ,podemos tomar por exemplo :
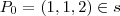
.O vetor diretor da reta

pode ser encontrado parametrizando a mesma ,ou encontrando outro ponto

para que
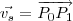
.
Em relação ao ponto

terá que impor
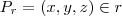
e
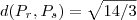
.
Acredito que estas informações sejam suficientes para prosseguir .
Tente concluir .


 .Considere
.Considere  ,respectivamente, vetor diretor da reta
,respectivamente, vetor diretor da reta  ,ponto arbitrário pertencente à reta
,ponto arbitrário pertencente à reta  (poderemos ter mais de um) e
(poderemos ter mais de um) e 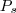 ponto da reta
ponto da reta  tal que
tal que 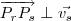 .
.  tal que
tal que  .
.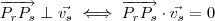 .
.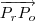 é combinação linear de
é combinação linear de  .
. 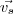 segue-se que :
segue-se que :  que devido ao item b) ,resulta :
que devido ao item b) ,resulta : 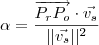 . Aplicando este resultado no item a) ,obtemos :
. Aplicando este resultado no item a) ,obtemos : 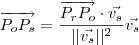 .
.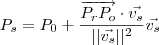 .
.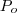 é arbitrário ,podemos tomar por exemplo :
é arbitrário ,podemos tomar por exemplo : 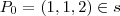 .O vetor diretor da reta
.O vetor diretor da reta  para que
para que 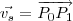 .
.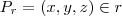 e
e 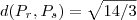 .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.