Me ajudem a resolver esses problemas por favor ! :
Primeiro problema -> Em um triângulo retângulo ABC , a diferença entre os catetos é 2 cm e o produto é 48 cm² . Calcule :
a) a hipotenusa deste triângulo
b) a altura relativa a hipotenusa .
c) as projeções dos catetos sobre a hipotenusa .
Segundo problema -> Na rua da esquina existia um poste com 5 metros de altura . Num dia de tempestade , o poste tombou embatendo numa janela que se encontra a um terço da altura do prédio onde morava João . Sabendo que a distância do poste ao edifício é de 2 metros , calcule a altura do prédio em causa.
obrigada.


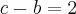

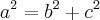










 .
.
 :
: