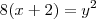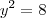por renan_a » Sex Nov 16, 2012 10:00
por renan_a » Sex Nov 16, 2012 10:00
Olá, estou com dúvida em dois exercícios de parábola, e para no enxer de tópicos, resolvi colocar os dois em um tópico.
1- Em que ponto a parábola de V(-2,0) e F (0,0) intercepta o eixo dos y
2- Encontrar sobre a parábola y²=4x um ponto tal que sua distância à diretriz seja igual a 3
Desde já , agradeço a quem me ajudar.
Abraço
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por young_jedi » Sex Nov 16, 2012 12:45
por young_jedi » Sex Nov 16, 2012 12:45
esta parabola é do tipo

o vertice esta em (h,k)=(0,0) e o foco (h+p,k)
portanto
h=-2,k=0,p=2
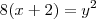
agora vamos ver onde ele cruza o eixo y (são os pontos onde x=0)


y=-4 ou y=4
______________________________________________________________________
2)
pela equação nos temos que
o vertcie (h,k)=(0,0)
p=1
então o foco
f(1,0)
então a reta diretriz esta em x=-1
então um ponto em que a distancia é igual a 3 sera
3=x-(-1)
x=2
portanto
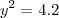
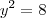

portano um ponto seria

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por renan_a » Sex Nov 16, 2012 13:20
por renan_a » Sex Nov 16, 2012 13:20
Valeu pela resposta, meu velho! =)
o número eu entendi.
Só que no dois eu fiquei meio boiando no que diz respeito ao V ser ( 0,0)...
A primeira coisa que eu descobri foi que o FOCO(1,0) , até aí beleza, mas o Vértice não poderia ser qualquer valor menor que x=1 ??
-------------------------------------------
Na parte em que tu fez: x-(-1)=3 -> x=2 , tu fez a equação da diretriz igual a 3? (x+1=3)
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por young_jedi » Sex Nov 16, 2012 14:40
por young_jedi » Sex Nov 16, 2012 14:40
no segundo chega -se a essa conclusão analisando a função

como a equação é

então chegamos a conculsão que p=1, k=0 e h=0
na parte da equação da diretriz
eu falei que a reta diretriz é x=-1
a distancia do vertice ao foco é igual a distancia da reta diretriz ao vertice
ai com a distancia tem que ser igual a 3 então um
ponto x pertencente a parabola tem que estar distante 3 unidades da reta x=-1
então
3=x-(-1)
3=x+1
x=2
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cônicas: Parábola]
por Ana_Rodrigues » Sáb Nov 19, 2011 11:39
- 1 Respostas
- 1618 Exibições
- Última mensagem por LuizAquino

Dom Nov 20, 2011 12:19
Geometria Analítica
-
- [cônicas] parábola
por renan_a » Qua Nov 14, 2012 19:23
- 2 Respostas
- 9650 Exibições
- Última mensagem por renan_a

Sex Nov 16, 2012 09:51
Geometria Analítica
-
- cônicas:equação da parabola
por may » Ter Jul 12, 2011 21:35
- 2 Respostas
- 11429 Exibições
- Última mensagem por may

Sex Jul 15, 2011 00:46
Geometria Analítica
-
- [Cônicas] O lugar geométrico dos vértices da parábola.
por Matheus Brito 2014 » Qui Set 10, 2015 22:40
- 1 Respostas
- 1574 Exibições
- Última mensagem por nakagumahissao

Sex Set 11, 2015 14:47
Geometria Analítica
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1524 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.