desenvolvimento satisfatório... por favor me ajudem
--> Uma lata cilíndrica está completamente cheia de determinado suco.
Esse líquido deve ser totalmente distribuído em x copos cilíndricos, cuja
altura é um quarto da altura da lata e o raio dois quintos do raio da lata.
Considerando-se que os copos ficaram totalmente cheios, pode-se
afirmar que o valor de x é:
a) 9
b) 16
c) 18
d) 25
e) 30
Até o momento eu tentei solucionar da seguinte forma:
A= R.H
(A)lata = x
(A)copo=

(R)lata = y
(R)copo=

Então:
Área da lata = xy
Área do copo:

e daí nao sei mais como desenvolver... se igualo as informações... ou o quê;;;
por favor me ajudem...



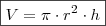

 é dado fazendo a divisão: volume da lata pelo volume do copo, isto é:
é dado fazendo a divisão: volume da lata pelo volume do copo, isto é: 
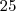 e você?
e você?
