 por iarapassos » Seg Set 03, 2012 17:47
por iarapassos » Seg Set 03, 2012 17:47
Ache uma equação do plano

que passa pelo ponto

, e é paralelo à reta

, e é perpendicular ao plano
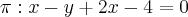
.
Por faor, deem-me dicas para conseguir resolver..
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Qua Set 05, 2012 16:24
por LuizAquino » Qua Set 05, 2012 16:24
iarapassos escreveu:Ache uma equação do plano

que passa pelo ponto

, e é paralelo à reta

, e é perpendicular ao plano
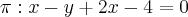
.
Por faor, deem-me dicas para conseguir resolver..
Pense um pouco... Se

e r são paralelos, então
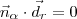
(com

um normal de

e
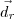
um diretor de r) . Por outro lado, se

e

são perpendiculares, então
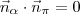
(com
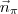
um normal de

) . Resumindo, note que você pode escolher
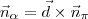
. Agora tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PLANOS - PARALELISMO ENTRE PLANOS
por ubelima » Ter Jun 19, 2012 19:22
- 2 Respostas
- 5836 Exibições
- Última mensagem por ubelima

Qua Jun 20, 2012 01:01
Geometria Analítica
-
- Mais uma de sequência
por Molina » Dom Mai 03, 2009 06:07
- 4 Respostas
- 2915 Exibições
- Última mensagem por lucasguedes

Ter Jul 07, 2009 21:08
Desafios Difíceis
-
- MAIS UMA QUESTÃO DE G.A
por GABRIELA » Ter Set 29, 2009 18:57
- 3 Respostas
- 2547 Exibições
- Última mensagem por Elcioschin

Qua Set 30, 2009 20:54
Geometria Analítica
-
- Mais uma questão
por GABRIELA » Seg Dez 07, 2009 17:16
- 1 Respostas
- 2200 Exibições
- Última mensagem por Elcioschin

Seg Dez 07, 2009 19:23
Estatística
-
- Mais um desafio..
por victoreis1 » Seg Nov 22, 2010 21:26
- 3 Respostas
- 2532 Exibições
- Última mensagem por Molina

Seg Nov 22, 2010 23:54
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 que passa pelo ponto
que passa pelo ponto  , e é paralelo à reta
, e é paralelo à reta  , e é perpendicular ao plano
, e é perpendicular ao plano 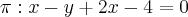 .
.
 que passa pelo ponto
que passa pelo ponto  , e é paralelo à reta
, e é paralelo à reta  , e é perpendicular ao plano
, e é perpendicular ao plano 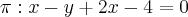 .
.
que passa pelo ponto
, e é paralelo à reta
, e é perpendicular ao plano
.
 e r são paralelos, então
e r são paralelos, então 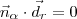 (com
(com  um normal de
um normal de  e
e 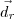 um diretor de r) . Por outro lado, se
um diretor de r) . Por outro lado, se  e
e  são perpendiculares, então
são perpendiculares, então 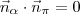 (com
(com 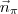 um normal de
um normal de  ) . Resumindo, note que você pode escolher
) . Resumindo, note que você pode escolher 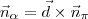 . Agora tente concluir o exercício.
. Agora tente concluir o exercício.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.