CarolMarques escreveu:Como se trata de uma parábola eu começo pela rotação dos eixos:

Utilizandos as fórmulas de rotação :
A'=0 C'=0 D'= -2 E'= 8
Aqui você cometeu um erro de digitação: o correto seria C' = 2.
CarolMarques escreveu:Substituindo:
2y'² -2x' +8y'+10=0
y'²+4y' -x'+10=0
Você cometeu outro erro de digitação: o correto seria y'² + 4y' - x' + 5 = 0.
CarolMarques escreveu:Completando os quadrados :
(y'+2)²=(x - 1)
Foi assim que eu fiz
Ainda com erros de digitação: seria (y' + 2)² = (x' - 1).
Fora os erros de digitação, o que você fez até aqui está correto: trata-se de uma parábola com vértice (1, -2). Mas note que esse vértice está no sistema x'Oy'. O que você obtém se escrevê-lo no sistema xOy?
ObservaçãoAinda falando sobre erros de digitação, a equação da cônica seria:
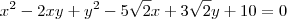
Note que você escreveu
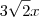
ao invés de
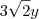
.
Eu vou aproveitar agora para dar algumas dicas sobre o
LaTeX.
No ambiente LaTeX, não use o atalho de teclado para a potência 2 (ou seja, "²"). Isso gera um erro que faz aparecer "²" na sua escrita. Ao invés disso use apenas "^2".
Exemplos
a) Código:
- Código: Selecionar todos
[tex]x²[/tex]
Resultado:
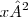
.
b) Código:
- Código: Selecionar todos
[tex]x^2[/tex]
Resultado:

.
Além disso, lembre-se que quando escrevemos uma raiz quadrada não é necessário colocar o índice "2". Sendo assim, use apenas algo como "\sqrt{a}" ou invés de "\sqrt[2]{a}".
Exemplos
a) Código:
- Código: Selecionar todos
[tex]\sqrt[2]{a}[/tex]
Resultado:
![\sqrt[2]{a} \sqrt[2]{a}](/latexrender/pictures/1b9b49e8f2fe06f8a8b891c700d41ec5.png)
.
b) Código:
- Código: Selecionar todos
[tex]\sqrt{a}[/tex]
Resultado:
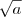
.
![x²-2xy+y²-5\sqrt[2]{2} x +3\sqrt[2]{2} x+10=0 x²-2xy+y²-5\sqrt[2]{2} x +3\sqrt[2]{2} x+10=0](/latexrender/pictures/1122555417b471f7d06ff8562ef776d5.png)
![(3\sqrt[2]{2} / 2 , - \sqrt[2]{2} /2 (3\sqrt[2]{2} / 2 , - \sqrt[2]{2} /2](/latexrender/pictures/77d8f0db5cc0b8f22a1eeb2d0a48894e.png)




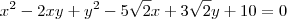
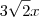 ao invés de
ao invés de 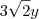 .
.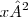 .
. .
.![\sqrt[2]{a} \sqrt[2]{a}](/latexrender/pictures/1b9b49e8f2fe06f8a8b891c700d41ec5.png) .
.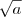 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.