Um paralelogramo de vértices A, B, C e D, tem lados AB e CD paralelos à reta de equação r: X=(0,0,0)+k(3,4,5) e os outros dois paralelos ao plano ? : x+y+3z=0. Conhecendo os vértices A e D, determine os vértices B e C. Dados: A=(0,0,0) e D=(1,1,1).
Resposta:
B=(15/22 , 20/22 , 25/22) e C=(7/22 , 2/22 , -3/22)
Achei estranho, pois se o lado AD pertence ao plano ?;, o vetor AD também deveria pertencer (AD // ?;), o que na realidade não acontece. (
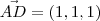 , 1.1+1.1+3.1 ?0).
, 1.1+1.1+3.1 ?0).Estou pensando de forma errônea?
Agradeço desde já.




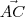 é paralelo ao plano
é paralelo ao plano  .
.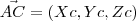 , temos a seguinte relação
, temos a seguinte relação (i)
(i) , donde tiramos:
, donde tiramos: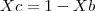
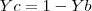
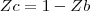
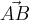 também é paralelo a r, sendo assim, temos a relação:
também é paralelo a r, sendo assim, temos a relação: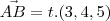 , sendo t um escalar (o vetor
, sendo t um escalar (o vetor 


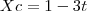
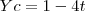
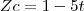
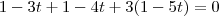
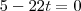
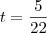
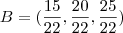 e
e 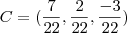
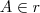 e
e 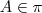 , temos que
, temos que  é paralelo a
é paralelo a 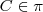 . Daí sim, fazendo
. Daí sim, fazendo 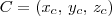 , como este ponto está no plano, temos que:
, como este ponto está no plano, temos que:

 .
.



