por Danilo » Qua Jul 11, 2012 05:40
por Danilo » Qua Jul 11, 2012 05:40
Pessoal, estou empacado em um exercício e quero muito saber onde estou errando.
Num triângulo ABC, no qual A(2,1), B(0,3) e C(-1,0), toma-se M na reta BC tal que as áreas dos triângulos AMC e AMB ficam na mesma razão 1/4. Calcular as coordenadas de M.
Resp.: M (-4/3,-1) ou M (-4/5,3/5)
Bom, SABC = área do triangulo ABC, SABM = área do triangulo ABM e S AMC = área do triangulo AMC. Primeiramente calculei a área do triângulo ABC e encontrei 4. De acordo com o enunciado, SAMB = 4SAMC. E também SABC = SABM + SAMC => 4 = 5SAMC => SAMC = 4/5 e SABC = 16/5 . Chamando o ponto M de (x,y) eu fiz o determinante do triângulo ABM e encontrei x-3y+1. Sua área é tal que x-3y+1 = 2SAMC. => x-3y+1 = 2(4/5) => x = (3+15y)/5. Analogamente, calculei a área do triângulo AMC tal que x = (-10y -2 )/10. Resolvendo o sistema formado pelas equações 3+15y)/5 e (-10y -2 )/10 eu consigo encontrar os valores de x e de y, mas esses valores encontrados não condizem com a resposta correta. Alguém poderia por favor me dizer onde estou errando? Agradeço mt a quem puder me ajudar. Valeu !
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Jul 11, 2012 09:47
por LuizAquino » Qua Jul 11, 2012 09:47
Danilo escreveu:Num triângulo ABC, no qual A(2,1), B(0,3) e C(-1,0), toma-se M na reta BC tal que as áreas dos triângulos AMC e AMB ficam na mesma razão 1/4. Calcular as coordenadas de M.
Resp.: M (-4/3,-1) ou M (-4/5,3/5)
Danilo escreveu:Pessoal, estou empacado em um exercício e quero muito saber onde estou errando.
Bom, SABC = área do triangulo ABC, SABM = área do triangulo ABM e S AMC = área do triangulo AMC. Primeiramente calculei a área do triângulo ABC e encontrei 4. De acordo com o enunciado, SAMB = 4SAMC. E também SABC = SABM + SAMC => 4 = 5SAMC => SAMC = 4/5 e SABC = 16/5 . Chamando o ponto M de (x,y) eu fiz o determinante do triângulo ABM e encontrei x-3y+1. Sua área é tal que x-3y+1 = 2SAMC. => x-3y+1 = 2(4/5) => x = (3+15y)/5. Analogamente, calculei a área do triângulo AMC tal que x = (-10y -2 )/10. Resolvendo o sistema formado pelas equações 3+15y)/5 e (-10y -2 )/10 eu consigo encontrar os valores de x e de y, mas esses valores encontrados não condizem com a resposta correta. Alguém poderia por favor me dizer onde estou errando? Agradeço mt a quem puder me ajudar. Valeu!
Basicamente você cometeu dois erros: 1) não necessariamente acontece SABC = SAMB + SAMC, pois o ponto M pode estar fora do segmento BC (a única restrição é que M deve estar na reta passando por BC); 2) as áreas de AMB e AMC estão erradas.
Considerando a reta r passando por B = (0, 3) e C = (-1, 0), obtemos r : y = 3x + 3. Como o ponto C está sobre essa reta, temos que o formato desse ponto é C = (t, 3t + 3), para algum escalar t.
Calculando as áreas SAMB e SAMC, obtemos:
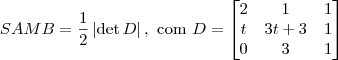
 Atenção!
Atenção! Note que
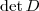
está dentro de um módulo. A imensa maioria das pessoas esquece disso quando aplica essa fórmula!
Fazendo as contas, obtemos então que:


Lembrando que SAMB = 4SAMC, podemos armar a seguinte equação modular:
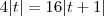
Agora basta você resolver essa equação modular. Você irá obter dois valores para t. Com isso, você obtém as duas possibilidades para C.
Tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Qua Jul 11, 2012 13:54
por Danilo » Qua Jul 11, 2012 13:54
LuizAquino escreveu:Danilo escreveu:Num triângulo ABC, no qual A(2,1), B(0,3) e C(-1,0), toma-se M na reta BC tal que as áreas dos triângulos AMC e AMB ficam na mesma razão 1/4. Calcular as coordenadas de M.
Resp.: M (-4/3,-1) ou M (-4/5,3/5)
Danilo escreveu:Pessoal, estou empacado em um exercício e quero muito saber onde estou errando.
Bom, SABC = área do triangulo ABC, SABM = área do triangulo ABM e S AMC = área do triangulo AMC. Primeiramente calculei a área do triângulo ABC e encontrei 4. De acordo com o enunciado, SAMB = 4SAMC. E também SABC = SABM + SAMC => 4 = 5SAMC => SAMC = 4/5 e SABC = 16/5 . Chamando o ponto M de (x,y) eu fiz o determinante do triângulo ABM e encontrei x-3y+1. Sua área é tal que x-3y+1 = 2SAMC. => x-3y+1 = 2(4/5) => x = (3+15y)/5. Analogamente, calculei a área do triângulo AMC tal que x = (-10y -2 )/10. Resolvendo o sistema formado pelas equações 3+15y)/5 e (-10y -2 )/10 eu consigo encontrar os valores de x e de y, mas esses valores encontrados não condizem com a resposta correta. Alguém poderia por favor me dizer onde estou errando? Agradeço mt a quem puder me ajudar. Valeu!
Basicamente você cometeu dois erros: 1) não necessariamente acontece SABC = SAMB + SAMC, pois o ponto M pode estar fora do segmento BC (a única restrição é que M deve estar na reta passando por BC); 2) as áreas de AMB e AMC estão erradas.
Considerando a reta r passando por B = (0, 3) e C = (-1, 0), obtemos r : y = 3x + 3. Como o ponto C está sobre essa reta, temos que o formato desse ponto é C = (t, 3t + 3), para algum escalar t.
Calculando as áreas SAMB e SAMC, obtemos:
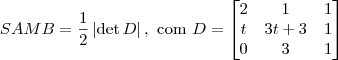
 Atenção!
Atenção! Note que
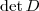
está dentro de um módulo. A imensa maioria das pessoas esquece disso quando aplica essa fórmula!
Fazendo as contas, obtemos então que:


Lembrando que SAMB = 4SAMC, podemos armar a seguinte equação modular:
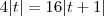
Agora basta você resolver essa equação modular. Você irá obter dois valores para t. Com isso, você obtém as duas possibilidades para C.
Tente concluir o exercício.
Muito obrigado = D
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo da area de um triangulo
por matway » Dom Set 04, 2011 20:36
- 2 Respostas
- 3043 Exibições
- Última mensagem por matway

Seg Set 05, 2011 09:04
Geometria Plana
-
- cálculo 1 area do triangulo
por ezidia51 » Qui Set 12, 2019 01:48
- 1 Respostas
- 3818 Exibições
- Última mensagem por adauto martins

Qua Out 02, 2019 16:54
Cálculo: Limites, Derivadas e Integrais
-
- [Triângulo] Calculo de área com integrais
por klueger » Qua Fev 06, 2013 18:10
- 1 Respostas
- 2107 Exibições
- Última mensagem por timoteo

Qua Fev 06, 2013 20:14
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida - Área do Triângulo
por Flordeliz » Sáb Nov 27, 2010 22:06
- 3 Respostas
- 2598 Exibições
- Última mensagem por Jefferson

Dom Nov 28, 2010 21:14
Geometria Plana
-
- [Cálculo de área de triângulo] Com os três eixos coordenado.
por Matheus Lacombe O » Sáb Out 13, 2012 16:30
- 1 Respostas
- 3450 Exibições
- Última mensagem por e8group

Sáb Out 13, 2012 17:51
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


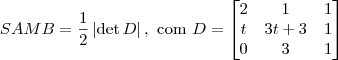

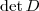 está dentro de um módulo. A imensa maioria das pessoas esquece disso quando aplica essa fórmula!
está dentro de um módulo. A imensa maioria das pessoas esquece disso quando aplica essa fórmula!