por Danilo » Sex Jun 22, 2012 21:14
Considere as retas r e s coplanares formando ângulos ? e ? com ? < ?. Pelo ponto de interseção passa uma reta t que forma com r um ângulo igual a (?+?/2). Quais os ângulos formados pelas retas t e s?
Esse problema eu nem sei como começar... pensei na equação de cada reta... pensei também na fórmula para calcular ângulos entre duas retas.. e não saio do lugar. Agradeço desde já se alguém puder dar uma luz. ^^
-
Danilo
- Colaborador Voluntário
-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
por Russman » Sáb Jun 23, 2012 18:58
Bom, eu encontrei
pi/2 - (? -?)/2 .
É este o gabarito?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário
-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
por Danilo » Sáb Jun 23, 2012 19:21
Russman escreveu:Bom, eu encontrei
pi/2 - (? -?)/2 .
É este o gabarito?
o gabarito é ?/2 + ? e ?/2 - ? !
-
Danilo
- Colaborador Voluntário
-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
por Russman » Sáb Jun 23, 2012 19:44
Bem, não sei se estou entendendo bem o que o exercicio pede.
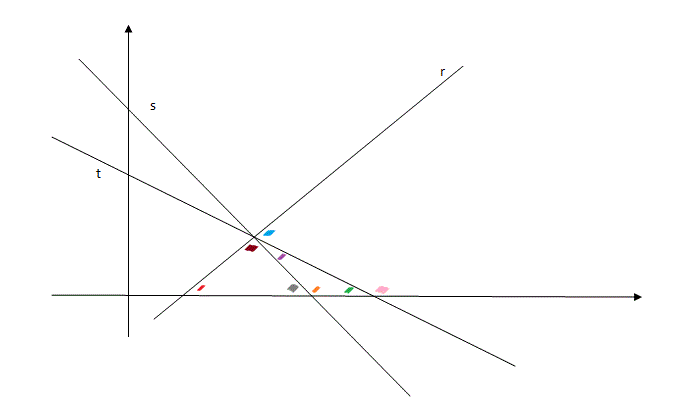
O ângulo vermelho é o ?, o laranja ?, e o azul claro (? +?)/2 . Vou chamar o roxo de w, que ao meu ver é o nosso interesse conhecê-lo, e de x o marrom.
Assim,
x + ? +pi -? = pi
x = ? - ?
Agora,
x+w+(? +?)/2 = pi ---------> w = pi/2 -( ? -?)/2 .
Não é esse angulo qe é pedido?
- Anexos
-
- ScreenHunter_01 Jun. 23 18.36.gif (5.6 KiB) Exibido 1505 vezes
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário
-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Angulos entre planos e retas] Piramide Regular
por LucasSG » Seg Jul 08, 2013 11:36
- 1 Respostas
- 1187 Exibições
- Última mensagem por young_jedi
Seg Jul 08, 2013 20:37
Geometria Analítica
-
- Ângulo entre duas retas
por Jonatan » Qui Jul 22, 2010 13:38
- 0 Respostas
- 3445 Exibições
- Última mensagem por Jonatan
Qui Jul 22, 2010 13:38
Geometria Analítica
-
- enconto entre duas retas
por matematicada » Qua Nov 24, 2010 12:14
- 2 Respostas
- 1562 Exibições
- Última mensagem por alexandre32100
Qua Nov 24, 2010 12:59
Funções
-
- Angulo Entre Duas Retas
por mayconf » Sex Set 21, 2012 13:33
- 2 Respostas
- 17573 Exibições
- Última mensagem por mayconf
Sex Set 21, 2012 18:09
Geometria Analítica
-
- Qual a distância entre as duas retas?
por welton » Qui Out 23, 2014 14:46
- 1 Respostas
- 4665 Exibições
- Última mensagem por DanielFerreira
Dom Jan 04, 2015 14:16
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
