 por Danilo » Qui Jun 14, 2012 06:15
por Danilo » Qui Jun 14, 2012 06:15
Dados os pontos A (a,0) e B (0,b), tomemos sobre a reta AB um ponto C de modo que BC = (m) x (AB) (m # 0 real). Pede-se a equação da reta perpendicular a AB, a qual passa pelo ponto médio do segmento AC.
Bom, a primeira coisa que fiz foi encontrar a equação da reta que passa por AB (reta que chamo de s) , que é b/ax- y - b. Sendo assim o coeficiente angular da reta que é perpendicular à reta s é -a/b. Bom, penso eu que agora só falta eu econtrar o ponto médio de AC. É aí que está o problema, não sei como encontrar... Sei que o ponto C está ''depois'' ou ''antes'' de AB pois BC = (m) x (AB) (m#0 real), me corrijam se eu estiver errado. Agradeço a qualquer ajuda. Valeu !
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sex Jun 15, 2012 20:29
por LuizAquino » Sex Jun 15, 2012 20:29
Danilo escreveu:Dados os pontos A (a,0) e B (0,b), tomemos sobre a reta AB um ponto C de modo que BC = (m) x (AB) (m # 0 real). Pede-se a equação da reta perpendicular a AB, a qual passa pelo ponto médio do segmento AC.
Danilo escreveu:Bom, a primeira coisa que fiz foi encontrar a equação da reta que passa por AB (reta que chamo de s) , que é b/ax- y - b. Sendo assim o coeficiente angular da reta que é perpendicular à reta s é -a/b. Bom, penso eu que agora só falta eu econtrar o ponto médio de AC. É aí que está o problema, não sei como encontrar... Sei que o ponto C está ''depois'' ou ''antes'' de AB pois BC = (m) x (AB) (m#0 real), me corrijam se eu estiver errado. Agradeço a qualquer ajuda. Valeu !
Primeiro, por favor procure usar a notação matemática correta. Por exemplo, não escreva "m # 0". Ao invés disso, escreva
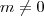
.
Para saber como digitar de forma adequada as notações matemáticas aqui no fórum, por favor vide o tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74Falando agora sobre sua resolução, a equação da reta s está errada. Na verdade a equação é

. Além do sinal para y estar errado, você esqueceu de digitar "= 0" em sua "equação" (note que não podemos nem chamar de equação o que você escreveu, já que não tem uma igualdade!).
Quanto ao ponto C, como
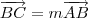
, temos que:



Agora tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Sáb Jun 16, 2012 03:22
por Danilo » Sáb Jun 16, 2012 03:22
Consegui resolver aqui. Mais uma vez, muito obrigado ! obs: vou tentar colocar as notações corretas e tentar não errar a álgebra. Valeu.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em exercício - Equação da reta
 por Danilo » Qui Mai 24, 2012 05:11
por Danilo » Qui Mai 24, 2012 05:11
- 5 Respostas
- 3934 Exibições
- Última mensagem por Danilo

Sáb Mai 26, 2012 18:59
Geometria Analítica
-
- [Equação de planos] Dúvida exercício
por MrJuniorFerr » Sáb Out 06, 2012 17:16
- 2 Respostas
- 3948 Exibições
- Última mensagem por MrJuniorFerr

Sáb Out 06, 2012 18:19
Geometria Analítica
-
- [Equação de planos] Dùvida exercício 2
por MrJuniorFerr » Sáb Out 06, 2012 20:39
- 14 Respostas
- 9063 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 19:07
Geometria Analítica
-
- [Equação de planos] Dùvida exercício 3
por MrJuniorFerr » Dom Out 07, 2012 02:49
- 3 Respostas
- 2331 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 17:21
Geometria Analítica
-
- [Equação de planos] Dúvida exercício 4
por MrJuniorFerr » Seg Out 08, 2012 07:40
- 1 Respostas
- 1336 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 10:06
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


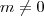 .
. . Além do sinal para y estar errado, você esqueceu de digitar "= 0" em sua "equação" (note que não podemos nem chamar de equação o que você escreveu, já que não tem uma igualdade!).
. Além do sinal para y estar errado, você esqueceu de digitar "= 0" em sua "equação" (note que não podemos nem chamar de equação o que você escreveu, já que não tem uma igualdade!).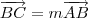 , temos que:
, temos que:


