 por Danilo » Sáb Jun 02, 2012 03:56
por Danilo » Sáb Jun 02, 2012 03:56
Pessoal, estou apanhando para resolver um exercício aparentemente simples... lá vai !
Qual é o valor de r para que a reta de equação x-5y+20=0 seja paralela à reta determinada pelos pontos M (r,s) e N (2,1)?
Bom, primeiro sei que, para que as retas sejam paralelas é necessário que x/r = -5/s ou que os coeficientes angulares das retas sejam iguais. Também sei que, se eu possuir um ponto dado (por exemplo (2,1)) e mais o coeficiente angular eu obtenho a equação da reta. tentei utilizar a equação y-y0=m(x-x0) mas eu não cheguei a lugar algum. Não estou conseguindo encaixar todas essas informações para resolver o problema ! Quem puder me dar uma luz, ou qual caminho seguir, agradeço !!!!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Sáb Jun 02, 2012 04:12
por Russman » Sáb Jun 02, 2012 04:12
Primeiro você deve identificar a reta que passa pelos pontos M e N analiticamente.
Esta reta é
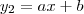
tal que,
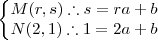
Solucionando este sistema identificamos a reta como

.
Como o coeficiente angular da outra reta é
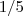
, então para satisfazer a condição de paralelismo, é fato que
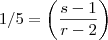
Ou seja,

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Danilo » Sáb Jun 02, 2012 04:30
por Danilo » Sáb Jun 02, 2012 04:30
Russman escreveu:Primeiro você deve identificar a reta que passa pelos pontos M e N analiticamente.
Esta reta é
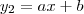
tal que,
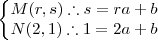
Solucionando este sistema identificamos a reta como

.
Como o coeficiente angular da outra reta é
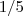
, então para satisfazer a condição de paralelismo, é fato que
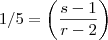
Ou seja,

.
Muito obrigado !
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida sobre Exercício Conjunto
por Jhosmy » Qua Jun 01, 2011 15:14
- 6 Respostas
- 3796 Exibições
- Última mensagem por Jhosmy

Sáb Jun 04, 2011 00:42
Conjuntos
-
- Dúvida sobre a resolução de um exercício
por Danilo » Qua Jul 25, 2012 12:15
- 1 Respostas
- 1401 Exibições
- Última mensagem por Danilo

Qua Jul 25, 2012 12:35
Álgebra Elementar
-
- [Probabilidade] Duvida sobre exercicio
por LsJack » Qui Ago 09, 2012 14:14
- 1 Respostas
- 1584 Exibições
- Última mensagem por fraol

Sáb Ago 11, 2012 12:34
Probabilidade
-
- Dúvida sobre resposta do exercício
por misaelbarreto » Dom Out 25, 2015 17:53
- 1 Respostas
- 1323 Exibições
- Última mensagem por misaelbarreto

Qui Out 29, 2015 00:44
Funções
-
- Exercício sobre equação da reta - Dúvida
 por Danilo » Seg Mai 07, 2012 00:28
por Danilo » Seg Mai 07, 2012 00:28
- 2 Respostas
- 1938 Exibições
- Última mensagem por Danilo

Dom Mai 13, 2012 22:38
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


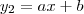 tal que,
tal que,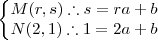
 .
.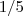 , então para satisfazer a condição de paralelismo, é fato que
, então para satisfazer a condição de paralelismo, é fato que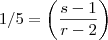
 .
.