 por Claudin » Sáb Abr 28, 2012 17:14
por Claudin » Sáb Abr 28, 2012 17:14
Tenho uma dúvida nesse conceito.
Teoricamente o vetor diretor, é perpendicular a reta, correto?
Pois então, quando tenho equação cartesiana como faço para encontrar os vetores diretores?
Por exemplo:
r1:
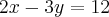
r2:

Posso afirmar que o vetor diretor da r1 seria, (3,-2) e da reta r2 seria (-3,-4)
Ou seja, para encontrar basta trocar a ordem dos números que multiplicam a incógnita e mudar o sinal?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Sáb Abr 28, 2012 18:05
por Russman » Sáb Abr 28, 2012 18:05
Nãao, o vetor diretor é
paralelo a reta!
Dado um ponto

pertencente a uma reta

e seja

um vetor diretor desta reta.
Assim,
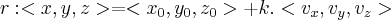
onde

é uma constante real qualquer.
A sua primeira reta é

. Parametrizando ela, isto é, tomando

e , portanto,

.
É possível demonstrar que o vetor diretor é dado pelos ceficientes de

das equ. paramétricas de reta.
Assim,
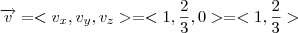
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Sáb Abr 28, 2012 18:15
por Russman » Sáb Abr 28, 2012 18:15
Veja que o vetor diretor não é somente este
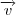
mas sim qualquer múltiplo real do mesmo.
Para calcular um vetor normal a reta, isto é, perpendicular a ela basta que ele seja perpendicular ao veotr diretor. Seja
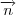
um vetor normal da reta

que tem como vetor diretor
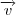
. Assim,
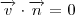
.
De onde,

.
Se tomarmos
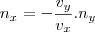
e
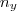
real solucionamos o problema!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Sáb Abr 28, 2012 18:25
por Claudin » Sáb Abr 28, 2012 18:25
Resumindo, o vetor diretor pode ser encontrado como eu disse acima?
Os vetores diretores no qual eu citei estão corretos?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Vetor diretor] Encontrando um vetor diretor
por amigao » Sex Mai 17, 2013 13:19
- 2 Respostas
- 8380 Exibições
- Última mensagem por amigao

Sáb Mai 18, 2013 20:12
Geometria Analítica
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4888 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
-
- [Curvas] Encontrar o vetor posição dado vetor aceleração
 por amigao » Sex Mai 09, 2014 16:37
por amigao » Sex Mai 09, 2014 16:37
- 1 Respostas
- 2079 Exibições
- Última mensagem por Russman

Sex Mai 09, 2014 17:25
Geometria Analítica
-
- Vetor
por cristina » Ter Mai 11, 2010 09:54
- 2 Respostas
- 1968 Exibições
- Última mensagem por cristina

Ter Mai 11, 2010 18:22
Geometria Analítica
-
- Vetor
por CarolMarques » Seg Jul 23, 2012 18:48
- 1 Respostas
- 3220 Exibições
- Última mensagem por LuizAquino

Seg Jul 23, 2012 19:54
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
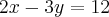



 pertencente a uma reta
pertencente a uma reta  e seja
e seja  um vetor diretor desta reta.
um vetor diretor desta reta.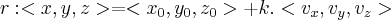
 é uma constante real qualquer.
é uma constante real qualquer. . Parametrizando ela, isto é, tomando
. Parametrizando ela, isto é, tomando  e , portanto,
e , portanto,  .
. das equ. paramétricas de reta.
das equ. paramétricas de reta.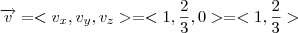 .
.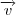 mas sim qualquer múltiplo real do mesmo.
mas sim qualquer múltiplo real do mesmo.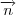 um vetor normal da reta
um vetor normal da reta 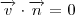 .
. .
.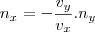 e
e 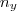 real solucionamos o problema!
real solucionamos o problema!




